Câu hỏi:
14/02/2025 714
Nhằm động viên, khen thưởng các em đạt danh hiệu “học sinh giỏi cấp thành phố” năm học 2024 – 2025, trường A tổ chức chuyến tham quan ngoại khóa tại một điểm du lịch với mức giá ban đầu là 375000 đồng/người. Biết công ty du lịch giảm 10 % chi phí cho mỗi giáo viên và giảm 30 % chi phí cho mỗi học sinh. Số học sinh nhiều hơn số giáo viên là 27 người và tổng chi phí\[{x^2} - {x^2} + 6x - 4x = 13 - 9\] tham quan (sau khi giảm giá) là \(12\,\,487\,\,500\) đồng. Tính số giáo viên và số học sinh đã tham gia chuyến đi.
Nhằm động viên, khen thưởng các em đạt danh hiệu “học sinh giỏi cấp thành phố” năm học 2024 – 2025, trường A tổ chức chuyến tham quan ngoại khóa tại một điểm du lịch với mức giá ban đầu là 375000 đồng/người. Biết công ty du lịch giảm 10 % chi phí cho mỗi giáo viên và giảm 30 % chi phí cho mỗi học sinh. Số học sinh nhiều hơn số giáo viên là 27 người và tổng chi phí\[{x^2} - {x^2} + 6x - 4x = 13 - 9\] tham quan (sau khi giảm giá) là \(12\,\,487\,\,500\) đồng. Tính số giáo viên và số học sinh đã tham gia chuyến đi.
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \[x\] (học sinh) là số lượng học sinh đi tham quan \(\left( {x \in \mathbb{N}*} \right).\)
Số lượng giáo viên đi tham quan là: \[x - 27\] (giáo viên).
Giá vé của mỗi học sinh là: \(\frac{x}{{36}}\) (người).
Do số shipper vận chuyển hàng giảm đi 3 người nên ta có phương trình:
\(\frac{x}{{30}} - \frac{x}{{36}} = 3\)
\[\left( {\frac{1}{{30}} - \frac{1}{{36}}} \right)x = 3\]
\(\frac{1}{{180}}x = 3\)
\(x = 540\) (thỏa mãn).
Vậy ngày 05/01/2025 công ty ABC giao cho khách 540 món hàng.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
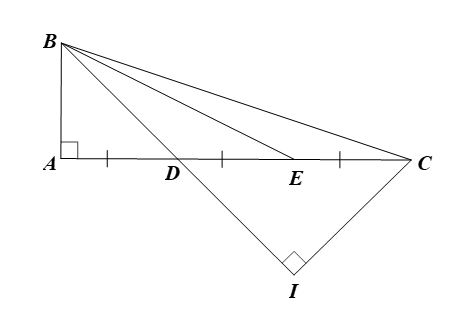
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = a,\) \(AC = 3a.\) Trên cạnh \(AC\) lấy các điểm \(D,\,\,E\) sao cho \(AD = DE = EC.\)
a) Tính các tỉ số \(\frac{{DB}}{{DE}},\,\,\frac{{DC}}{{DB}}.\)
b) Chứng minh
c) Tính \(\widehat {AEB} + \widehat {ACB}.\)
d) Qua \(C\) kẻ đường thẳng vuông góc với \(BD\) và cắt \(BD\) tại \(I.\) Chứng minh \(BD \cdot BI + CD \cdot CA = B{C^2}.\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = a,\) \(AC = 3a.\) Trên cạnh \(AC\) lấy các điểm \(D,\,\,E\) sao cho \(AD = DE = EC.\)
a) Tính các tỉ số \(\frac{{DB}}{{DE}},\,\,\frac{{DC}}{{DB}}.\)
b) Chứng minh
c) Tính \(\widehat {AEB} + \widehat {ACB}.\)
d) Qua \(C\) kẻ đường thẳng vuông góc với \(BD\) và cắt \(BD\) tại \(I.\) Chứng minh \(BD \cdot BI + CD \cdot CA = B{C^2}.\)
Xem đáp án »
14/02/2025
584
Câu 2:
Cho biểu thức \(P = \left( {\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{{{x^2} - 3x}}{{{x^2} - 1}}} \right) \cdot \frac{{x + 4}}{x}.\)
a) Viết điều kiện xác định của biểu thức \(P.\)
b) Rút gọn biểu thức \(P.\)
c) Tìm số nguyên \(x\) để \(P\) nhận giá trị nguyên.
Cho biểu thức \(P = \left( {\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{{{x^2} - 3x}}{{{x^2} - 1}}} \right) \cdot \frac{{x + 4}}{x}.\)
a) Viết điều kiện xác định của biểu thức \(P.\)
b) Rút gọn biểu thức \(P.\)
c) Tìm số nguyên \(x\) để \(P\) nhận giá trị nguyên.
Xem đáp án »
14/02/2025
194
Câu 3:
Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?
Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?
Xem đáp án »
14/02/2025
139
Câu 4:
Một công ty may mặc phải sản xuất \(10\,\,000\) sản phẩm trong \(x\) ngày. Khi thực hiện không những đã làm xong sớm một ngày mà còn làm thêm được \(80\) sản phẩm. Hãy biểu diễn qua \(x:\)
a) Số sản phẩm phải sản xuất trong một ngày theo kế hoạch.
b) Số lượng sản phẩm thực tế đã làm được trong một ngày.
Một công ty may mặc phải sản xuất \(10\,\,000\) sản phẩm trong \(x\) ngày. Khi thực hiện không những đã làm xong sớm một ngày mà còn làm thêm được \(80\) sản phẩm. Hãy biểu diễn qua \(x:\)
a) Số sản phẩm phải sản xuất trong một ngày theo kế hoạch.
b) Số lượng sản phẩm thực tế đã làm được trong một ngày.
Xem đáp án »
14/02/2025
66
Câu 5:
Giải các phương trình sau:
a) \(15 - 4x = x - 5\). b) \[x - 3\left( {2 - x} \right) = 2x - 4.\]
c) \(\frac{{7x - 1}}{6} = \frac{{16 - x}}{5} - 2x.\) d) \[{\left( {x + 3} \right)^2} - 13 = x\left( {x + 4} \right).\]
Giải các phương trình sau:
a) \(15 - 4x = x - 5\). b) \[x - 3\left( {2 - x} \right) = 2x - 4.\]
c) \(\frac{{7x - 1}}{6} = \frac{{16 - x}}{5} - 2x.\) d) \[{\left( {x + 3} \right)^2} - 13 = x\left( {x + 4} \right).\]
Xem đáp án »
14/02/2025
49
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
10 Bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận