Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Theo kế hoạch 2 tổ phải sản xuất 700 sản phẩm. Nhưng do tổ 1 làm vượt mức 15% và tổ 2 vượt mức 20% so với kế hoạch nên cả 2 tổ làm được 820 sản phẩm. Tính số sản phẩm mỗi tổ phải làm theo kế hoạch?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp số: 20.
Gọi \(x\)(cây) là số cây mỗi ngày công nhân trồng theo dự kiến \[\left( {x \in \mathbb{N}*} \right).\]
Thời gian trồng cây theo dự kiến là :\(\frac{{300}}{x}\)(ngày)
Thực tế, số cây trồng được mỗi ngày là \(x + 5\)(cây)
Thời gian trồng cây thực tế là :\(\frac{{300}}{{x + 5}}\)(ngày)
Theo đề bài ta có phương trình \(\frac{{300}}{x} - \frac{{300}}{{x + 5}} = 3\)
\(300\left( {x + 5} \right) - 300x = 3x\left( {x + 5} \right)\)
\(300x + 1500 - 300x = 3{x^2} + 15x\)
\(3{x^2} + 15x - 1500 = 0\)
\[{x^2} + 5x - 500 = 0\]
\[x = 20\] (TMĐK) hoặc \[x = - 25\] (loại).
Vậy mỗi ngày dự kiến trồng được 20 cây.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
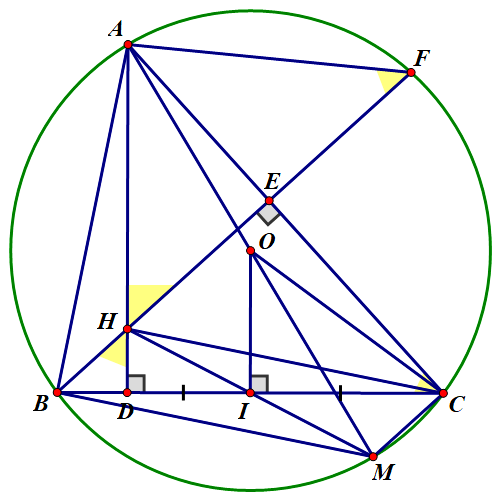
a) Gọi \(O'\) là trung điểm của cạnh \[CH.\]
Ta có \(HD \bot CD\) nên \(\widehat {HDC} = 90^\circ \).
Xét \(\Delta HDC\)vuông tại \[D\] có \(DO'\) là trung tuyến nên \(DO' = HO' = CO' = \frac{1}{2}HC\).
Chứng ming tương tự, ta có \(CO' = HO' = EO' = \frac{1}{2}HC\).
Do đó \(DO' = HO' = CO' = EO' = \frac{1}{2}HC\).
Vậy bốn điểm \(D,\,\,H,\,\,E,\,\,C\) cùng thuộc một đường tròn.
Vậy tứ giác \(DHEC\) nội tiếp đường tròn.
b) Trong tam giác \(ABC\) có \(BE,\,\,AD\) là hai đường cao cắt nhau tại \(H\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên \(CH \bot AB\).
Trong\(\left( O \right)\) có \(\widehat {ABM},\,\,\widehat {ACM}\) là hai góc nội tiếp cùng chắn nửa đường tròn đường kính \(AM\).
Suy ra \(\widehat {ABM} = \widehat {ACM} = 90^\circ \) nên \(MB \bot AB\,;\,\,MC \bot AC.\)
Mà \(CH \bot AB\,;\,\,BH \bot AC\) nên \(MB\,{\rm{//}}\,CH,\,\,MC\,{\rm{//}}\,BH\) nên \(BHCM\) là hình bình hành.
Xét đường tròn \(\left( O \right)\) có \(OI \bot BC\) tại \(I\) nên \(I\) là trung điểm của \(BC\) (đường kính vuông góc với dây).
c) Xét \(\Delta DHB\) và \(\Delta DCA\) có
\(\widehat {BDH} = \widehat {ADC} = 90^\circ \) (vì \(AD \bot BC\))
\(\widehat {HBD} = \widehat {DAC}\) (cùng phụ \(\widehat {ACB}\))
Do đó .
Suy ra \(\frac{{DH}}{{DC}} = \frac{{DB}}{{DA}}\) hay \(DH \cdot DA = DB \cdot DC.\)
Ta có \({\left( {a - b} \right)^2} \ge 0\) hay \({a^2} - 2ab + {b^2} \ge 0\) nên \({a^2} + 2ab + {b^2} \ge 4ab\), suy ra \(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\).
Áp dụng bất đẳng thức \(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\), ta có: \(DB \cdot DC \le \frac{{{{\left( {DB + DC} \right)}^2}}}{4} = \frac{{B{C^2}}}{4}\).
Suy ra \(DH \cdot DA \le \frac{{B{C^2}}}{4}\) không đổi vì \(BC\) cố định.
Dấu xảy ra khi \(DB = DC\), khi đó \(A\) là điểm chính giữa cung lớn .
Vậy \(A\) là điểm chính giữa cung lớn thì giá trị lớn nhất của \(DH \cdot DA\) bằng \(\frac{{B{C^2}}}{4}\).
Lời giải
Hướng dẫn giải
Đáp án: a) Sai.b) Đúng.c) Sai.d) Sai.
⦁ Thể tích hình trụ có bán kính đáy \(R\) và chiều cao \(h\), được tính bằng công thức: \(V = \pi {R^2}h.\)
Do đó ý a) là sai.
⦁ Đường kính đáy là \[4,4{\rm{ cm}}\] nên bán kính đáy \(R = \frac{{4,4}}{2} = 2,2\,\,\left( {{\rm{cm}}} \right)\). Do đó ý b) là đúng.
⦁ Thể tích của que kem là: \({V_1} = \frac{1}{3}\pi \cdot {\left( {2,2} \right)^2} \cdot 12 = \frac{{484}}{{25}}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\) Do đó ý c) là sai.
⦁ Thể tích hình trụ là: \({V_2} = 100\pi \cdot 15 = 1500\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Số chiếc kem ốc quế tối đa có thể làm được là: \(\frac{{1500\pi }}{{\frac{{484}}{{25}}\pi }} = \frac{{9375}}{{121}} \approx 77\) (cái). Do đó ý d) là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[T = 1\].
B. \[T = 2.\]
C. \[T = 3.\]
D. \[T = 4.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.