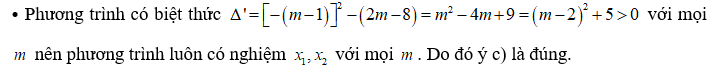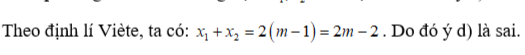Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho phương trình ( m là tham số, x là biến số).
a) Phương trình đã cho là phương trình bậc hai một ẩn.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho phương trình ( m là tham số, x là biến số).
Quảng cáo
Trả lời:
Đúng
Câu hỏi cùng đoạn
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
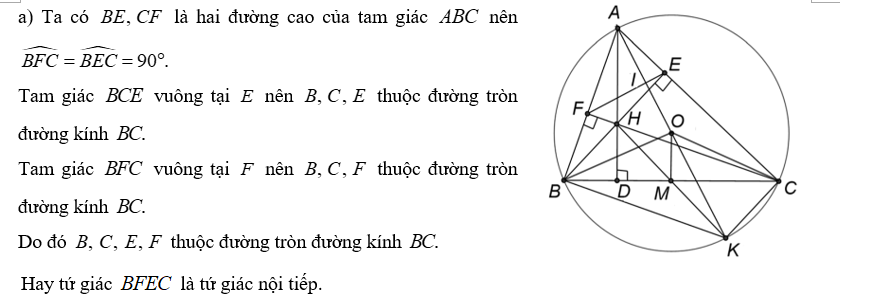
Bài 2. (1,5 điểm) Cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn (O;R). Các đường cao BE;CF của tam giác cắt nhau tại H (E thuộc AC , F thuộc AB).
a) Chứng minh: Tứ giác BFEC nội tiếp đường tròn.
b) Kẻ đường kính AK của đường tròn (O). Chứng minh AK vuông góc với È.
c) Giả sử BC cố định và A di chuyển trên cung lớn BC sao cho tam giác ABC luôn là tam giác nhọn. Xác định vị trí của điểm A để diện tích tam giác EAH lớn nhất. Tính giá trị lớn nhất đó theo R khi
Bài 2. (1,5 điểm) Cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn (O;R). Các đường cao BE;CF của tam giác cắt nhau tại H (E thuộc AC , F thuộc AB).
a) Chứng minh: Tứ giác BFEC nội tiếp đường tròn.
b) Kẻ đường kính AK của đường tròn (O). Chứng minh AK vuông góc với È.
c) Giả sử BC cố định và A di chuyển trên cung lớn BC sao cho tam giác ABC luôn là tam giác nhọn. Xác định vị trí của điểm A để diện tích tam giác EAH lớn nhất. Tính giá trị lớn nhất đó theo R khi
Lời giải


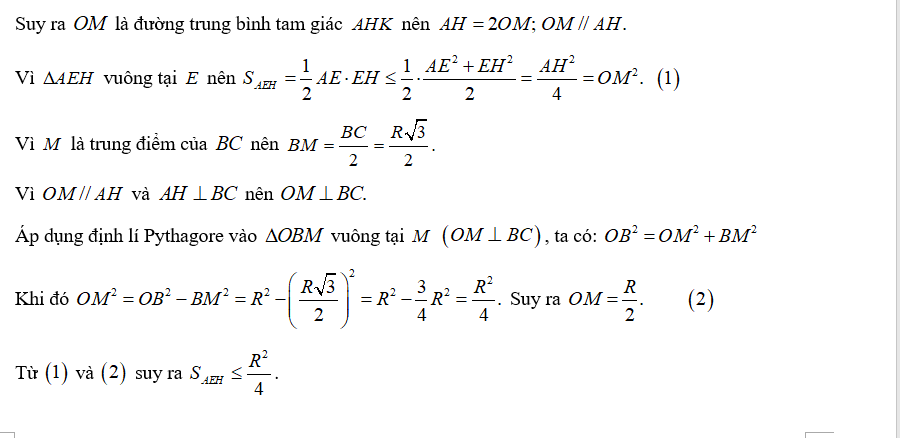
Lời giải
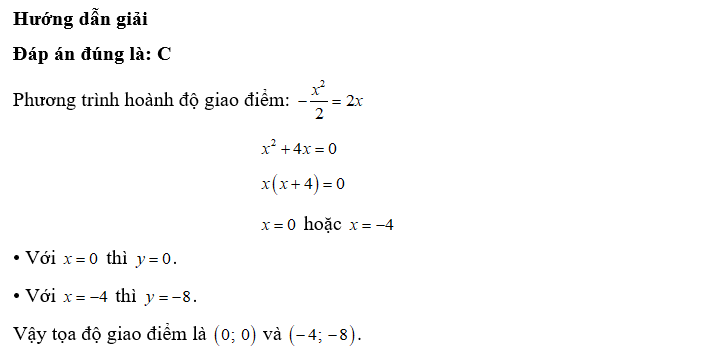
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.