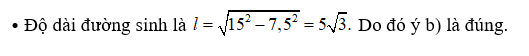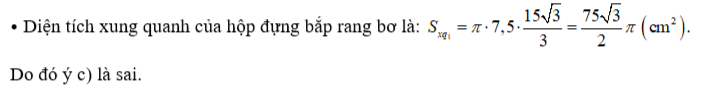Một quầy hàng A đựng bắp rang bơ vào một loại hộp có dạng hình nón với kích thước như hình vẽ.
Quầy hàng B đựng bắp rang bơ vào một loại hộp có dạng hình trụ có đáy và chiều cao bằng với loại hộp hình nón mà quầy A đã dùng. Biết giá 1 hộp bắp rang bơ của quầy A và quầy B bán lần lượt là 50 000 đồng và 100 đồng.

a) Diện tích xung quanh của hình nón có bán kính đáy R và đường sinh được tính bằng công thức:
Một quầy hàng A đựng bắp rang bơ vào một loại hộp có dạng hình nón với kích thước như hình vẽ.
Quầy hàng B đựng bắp rang bơ vào một loại hộp có dạng hình trụ có đáy và chiều cao bằng với loại hộp hình nón mà quầy A đã dùng. Biết giá 1 hộp bắp rang bơ của quầy A và quầy B bán lần lượt là 50 000 đồng và 100 đồng.

Quảng cáo
Trả lời:

Câu hỏi cùng đoạn
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Bài 2. (1,5 điểm) Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.
b) Chứng minh KH song song với ED và tam giác ACF là tam giác cân.
c) Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.
Bài 2. (1,5 điểm) Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.
b) Chứng minh KH song song với ED và tam giác ACF là tam giác cân.
c) Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.
Lời giải



Lời giải
Chọn B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.