Khối 12 có 12 học sinh xuất sắc trong đó có 6 nam. Khối 11 có 15 học sinh xuất sắc trong đó có 7 nam. Khối 10 có 10 học sinh xuất sắc trong đó có 4 nam. Nhân dịp tổng kết cuối năm học, nhà trường chọn ngẫu nhiên 3 học sinh để trao thưởng. Tính xác suất sao cho mỗi khối có ít nhất 1 học sinh và có cả học sinh nam lẫn học sinh nữ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Ta có \(n\left( \Omega \right) = C_{37}^3\).
Gọi biến cố \(A:\) “Mỗi khối có ít nhất 1 học sinh và có cả học sinh nam lẫn học sinh nữ”.
Chọn 3 học sinh sao cho mỗi khối có ít nhất 1 học sinh có \(C_{12}^1.C_{15}^1.C_{10}^1 = 1800\) cách.
Chọn 3 học sinh sao cho mỗi khối có ít nhất 1 học sinh và toàn học sinh nam có \(C_6^1.C_7^1.C_4^1 = 168\) cách.
Chọn 3 học sinh sao cho mỗi khối có ít nhất 1 học sinh và toàn học sinh nữ có \(C_6^1.C_8^1.C_6^1 = 288\) cách.
Suy ra \(n\left( A \right) = 1800 - 168 - 288 = 1344\).
Do đó \(P\left( A \right) = \frac{{1344}}{{1800}} = \frac{{56}}{{75}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(P\left( \emptyset \right) = 0\).
B. \(0 < P\left( A \right) < 1\).
C. \(P\left( \Omega \right) = 1\).
D. \(P\left( A \right) + P\left( {\overline A } \right) = 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: B
\(0 \le P\left( A \right) \le 1\).
Câu 2
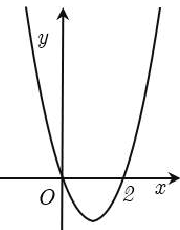
A. \(x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\).
B. \(x \in \left( {0;2} \right)\).
C. \(x \in \mathbb{R}\).
D. \(x \in \left( {2; + \infty } \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Dựa vào đồ thị hàm số ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập