Câu hỏi:
06/04/2025 1,225
Câu 10-11. (1,5 điểm) Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít ba quả bóng tennis xếp theo chiều dọc (hình vẽ). Các quả bóng tennis có dạng hình cầu, đường kính \(6,4\;{\rm{cm}}\).
a) Tính thể tích hộp dựng bóng (bỏ qua bề dày của vỏ hộp, làm tròn kết quả đến hàng đơn vị của \({\rm{c}}{{\rm{m}}^3}\)).
Câu 10-11. (1,5 điểm) Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít ba quả bóng tennis xếp theo chiều dọc (hình vẽ). Các quả bóng tennis có dạng hình cầu, đường kính \(6,4\;{\rm{cm}}\).
a) Tính thể tích hộp dựng bóng (bỏ qua bề dày của vỏ hộp, làm tròn kết quả đến hàng đơn vị của \({\rm{c}}{{\rm{m}}^3}\)).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chiều cao hộp dựng bóng hình trụ là \(h = 6,4 \cdot 3 = 19,2\,\,(\;{\rm{cm}})\)
Bán kính đáy hộp đựng bóng hình trụ là \({R_1} = 6,4:2 = 3,2\,\,(\;{\rm{cm}})\).
Thể tích hộp đựng bóng hình trụ là:
\({V_1} = \pi rR_1^2\;h = \pi \cdot 3,{2^2} \cdot 19,2 = 618\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
Vậy thể tích hộp dựng bóng \(618\,\,{\rm{c}}{{\rm{m}}^3}.\)
Câu hỏi cùng đoạn
Câu 2:
b) Tính thể tích bên trong hộp đựng bóng không bị chiếm bởi ba quả bóng tennis.
Lời giải của GV VietJack
Bán kính quả bóng tennis là \({R_2} = \frac{{6,4}}{2} = 3,2\,\,\left( {cm} \right)\).
Thể tích của ba quả bóng tennis có dạng hình cầu là:
\({V_2} = 3.\left( {\frac{4}{3}\pi R_2^3} \right) = 3 \cdot \left( {\frac{4}{3}\pi \cdot 3,{2^3}} \right) \approx 412\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích bên trong hộp đựng bóng không bị chiếm bởi ba quả bóng tennis là:
\(V = {V_1} - {V_2} = 618 - 412 = 206\,\,\left( {c{m^3}} \right)\).
Vậy thể tích bên trong hộp đựng bóng không bị chiếm bởi ba quả bóng tennis \(206\,\,c{m^3}.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Kí hiểu \[T\] là màu trắng, là màu đỏ và \[V\] là màu vàng.
Không gian mẫu .
Do đó, không gian mẫu có 4 phần tử.
Lời giải
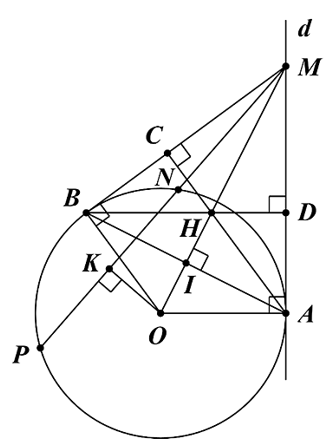
a) Ta có \(\widehat {OAM} = 90^\circ \) (do \[MA\] là tiếp tuyến của \[\left( O \right)\], \[A\] là tiếp điểm).
Suy ra ba điểm \(O,\,\,A,\,\,M\) cùng thuộc một đường tròn đường kính \[OM. & \left( 1 \right)\]
Lại có \(\widehat {OBM} = 90^\circ \) (do \[MB\] là tiếp tuyến của \[\left( O \right)\], \[B\] là tiếp điểm).
Suy ra ba điểm \(O,\,\,B,\,\,M\) cùng thuộc một đường tròn đường kính \[OM. & \left( 2 \right)\]Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta được tứ giác \[AMBO\] nội tiếp đường tròn đường kính \[OM.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận