Câu 1-2. Cho đồ thị hàm số \(\left( P \right):y = 5{x^2}\). Xác định điểm thuộc đồ thị hàm số \(\left( P \right)\) thỏa mãn:
a) Điểm đó có hoành độ bằng \( - 2.\)
Câu 1-2. Cho đồ thị hàm số \(\left( P \right):y = 5{x^2}\). Xác định điểm thuộc đồ thị hàm số \(\left( P \right)\) thỏa mãn:
a) Điểm đó có hoành độ bằng \( - 2.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét đồ thị hàm số \(y = 5{x^2}\).
a) Với \(x = - 2\) thì \(y = 5 \cdot {\left( { - 2} \right)^2} = 20.\)
Vậy tọa độ điểm cần tìm là \(\left( { - 2\,;\,\,20} \right).\)
Câu hỏi cùng đoạn
Câu 2:
b) Điểm đó có tung độ bằng 5.
b) Điểm đó có tung độ bằng 5.
Giải bởi Vietjack
b) Với \(x = 5\) thì \(5{x^2} = 5\) nên \({x^2} = 1.\)
Do đó \(x = 1\) hoặc \(x = - 1.\)
Vậy có hai điểm thỏa mãn yêu cầu bài toán là \(\left( {1\,;\,\,5} \right)\) hoặc \(\left( { - 1\,;\,\,5} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
2. Gọi \(x\,\,\left( {\rm{\% }} \right)\) là lãi suất trong một năm của ngân hàng \(\left( {x > 0} \right)\).
Sau năm thứ nhất người đó phải trả:
\(20\,\,000\,\,000 + 20\,\,000\,\,000 \cdot \frac{x}{{100}} = 200\,\,000\left( {100 + x} \right)\)
Số tiền sau năm thứ hai tăng thêm là:
\(200\,\,000\left( {100 + x} \right)\frac{x}{{100}} = 2\,\,000x\left( {x + 100} \right)\)
Theo bài ra, ta có phương trình:
\(200\,\,000\left( {100 + x} \right) + 2\,\,000x\left( {x + 100} \right) = 24\,\,200\,\,000\)
\(100\left( {100 + x} \right) + x\left( {x + 100} \right) = 12\,\,100\)
\({x^2} + 200x - 2\,\,100\,\,000 = 0\)
\(x = 10\) (TMĐK) hoặc \(x = - 210\) (loại).
Vậy lãi của ngân hàng một năm là \(10{\rm{\% }}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
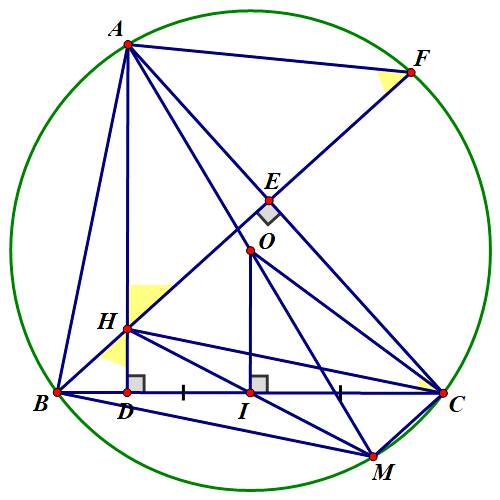
a) Gọi \(O'\) là trung điểm của cạnh \[CH.\]
Ta có \(HD \bot CD\) nên \(\widehat {HDC} = 90^\circ \).
Xét \(\Delta HDC\)vuông tại \[D\] có \(DO'\) là trung tuyến nên \(DO' = HO' = CO' = \frac{1}{2}HC\).
Chứng ming tương tự, ta có
\(CO' = HO' = EO' = \frac{1}{2}HC\).
Do đó \(DO' = HO' = CO' = EO' = \frac{1}{2}HC\).Do đó, bốn điểm \(D,\,\,H,\,\,E,\,\,C\) cùng thuộc một đường tròn.
Vậy tứ giác \(DHEC\) nội tiếp đường tròn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập