Câu 5-6. Cho đồ thị hàm số \(\left( P \right):y = 5{x^2}\). Xác định điểm thuộc đồ thị hàm số \(\left( P \right)\) thỏa mãn:
a) Điểm đó có hoành độ bằng \( - 2.\)
Câu 5-6. Cho đồ thị hàm số \(\left( P \right):y = 5{x^2}\). Xác định điểm thuộc đồ thị hàm số \(\left( P \right)\) thỏa mãn:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét đồ thị hàm số \(y = 5{x^2}\).
a) Với \(x = - 2\) thì \(y = 5 \cdot {\left( { - 2} \right)^2} = 20.\)
Vậy tọa độ điểm cần tìm là \(\left( { - 2\,;\,\,20} \right).\)
Câu hỏi cùng đoạn
Câu 2:
b) Điểm đó có tung độ bằng 5.
Giải bởi Vietjack
b) Với \(x = 5\) thì \(5{x^2} = 5\) nên \({x^2} = 1.\)
Do đó \(x = 1\) hoặc \(x = - 1.\)
Vậy có hai điểm thỏa mãn yêu cầu bài toán là \(\left( {1\,;\,\,5} \right)\) hoặc \(\left( { - 1\,;\,\,5} \right).\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Kí hiểu \[T\] là màu trắng, là màu đỏ và \[V\] là màu vàng.
Không gian mẫu .
Số kết quả có thể xảy ra là \(n\left( \Omega \right) = 4\).
Lời giải
b) Bảng tần số tương đối của mỗi nhóm
|
Nhóm |
\[\left[ {36\,;\,38} \right)\] |
\[\left[ {38\,;40} \right)\] |
\[\left[ {40\,;42} \right)\] |
\[\left[ {42\,;\,44} \right)\] |
\[\left[ {44\,;46} \right)\] |
|
Tần số tương đối \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
Biểu đồ cột của mẫu số liệu ghép nhóm:
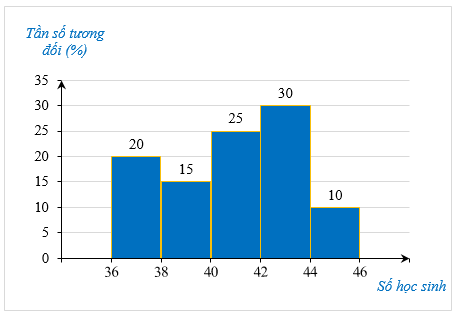
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo