Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right),\] vẽ các đường cao \[BD\] và \[CE.\]
a) Chứng minh:
Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right),\] vẽ các đường cao \[BD\] và \[CE.\]
a) Chứng minh:
Quảng cáo
Trả lời:
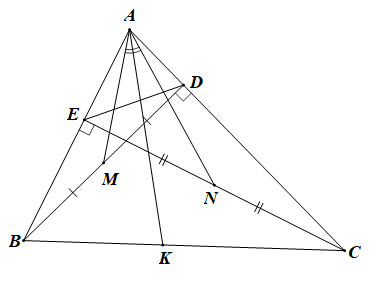
a) Xét \[\Delta ABD\] và \[\Delta ACE\] có:
\[\widehat {BAC}\] chung, \[\widehat {ADB} = \widehat {AEC} = 90^\circ \] (gt)
Suy ra (g.g)Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh: \(\widehat {ABC} + \widehat {EDC} = 180^\circ \).
b) Chứng minh: \(\widehat {ABC} + \widehat {EDC} = 180^\circ \).
Vì (câu a) nên \[\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\] (các cặp cạnh tương ứng tỉ lệ).
\[\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\] (chứng minh trên); \[\widehat {BAC}\] chung.
Do đó (c.g.c)
Suy ra \[\widehat {ADE} = \widehat {ABC}\] (hai góc tương ứng)
Mặc khác \[\widehat {ADE} + \widehat {EDC} = 180^\circ \] (hai góc kề bù)
Do đó \[\widehat {ADE} + \widehat {EDC} = \widehat {ABC} + \widehat {EDC} = 180^\circ \].
Vậy \[\widehat {ABC} + \widehat {EDC} = 180^\circ .\]
Câu 3:
c) Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của đoạn thẳng \[BD\] và \[CE.\] Vẽ \[AK\] là phân giác của \[\widehat {MAN}\,\,(K \in BC).\] Chứng minh \[KB \cdot AC = KC \cdot AB.\]
c) Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của đoạn thẳng \[BD\] và \[CE.\] Vẽ \[AK\] là phân giác của \[\widehat {MAN}\,\,(K \in BC).\] Chứng minh \[KB \cdot AC = KC \cdot AB.\]
c) Vì (câu a) nên \(\frac{{AB}}{{AC}} = \frac{{BD}}{{CE}}\) (tỉ số đồng dạng).
Mà \[M,{\rm{ }}N\] lần lượt là trung điểm của đoạn thẳng \[BD\] và \[CE\] nên \[BD = 2BM\] và \[CE = 2CN.\]
Suy ra \(\frac{{AB}}{{AC}} = \frac{{BD}}{{CE}} = \frac{{2BM}}{{2CN}} = \frac{{BM}}{{CN}}.\)
Xét \[\Delta ABM\] và \[\Delta ACN\] có:
\(\frac{{AB}}{{AC}} = \frac{{BM}}{{CN}}\) (chứng minh trên)
\(\widehat {ABM} = \widehat {ACN}\) (do cùng phụ với \(\widehat {BAC}\))
Do đó ( c.g.c)Suy ra \[\widehat {BAM} = \widehat {CAN}\] (hai góc tương ứng)
Lại có AK là tia phân giác của \(\widehat {MAN}\) (giả thiết)
Suy ra \[\widehat {MAK} = \widehat {NAK}\] (tính chất tia phân giác của một góc)
Do đó \[\widehat {BAM} + \widehat {MAK} = \widehat {CAN} + \widehat {NAK}\] hay \(\widehat {BAK} = \widehat {KAC}\)
Nên \[AK\] là tia phân giác của \(\widehat {BAC}\).
Theo tính chất tia phân giác của tam giác ta có: \(\frac{{AB}}{{AC}} = \frac{{KB}}{{KC}}\).
Do đó \[KB \cdot AC = KC \cdot AB\] (điều phải chứng minh).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
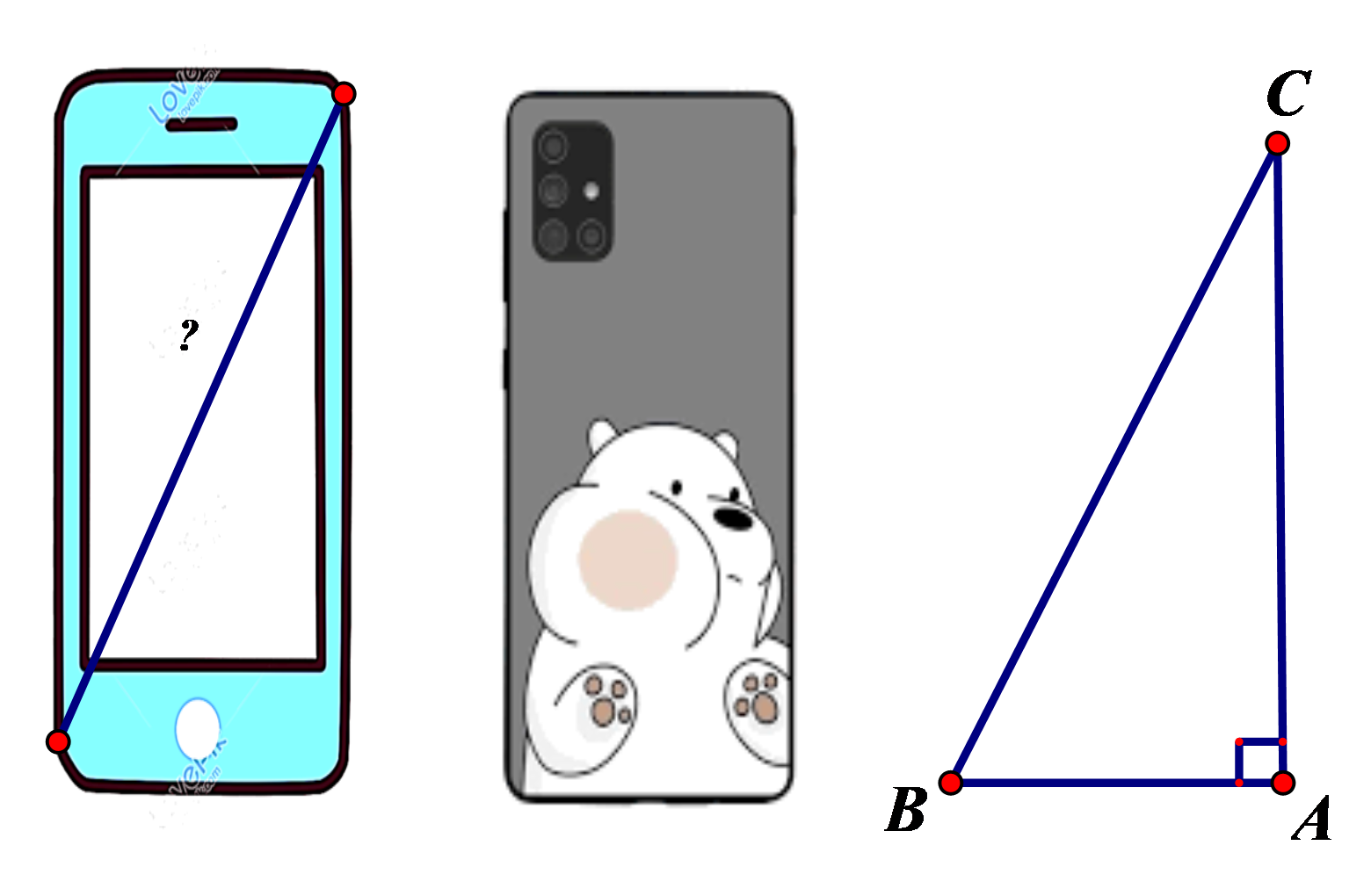
Áp dụng định lí Pythagore vào tam giác \[ABC\] vuông tại \[A\], ta có:
\(B{C^2} = A{C^2} + A{B^2} = {\left( {15,5} \right)^2} + {7^2} = 289,25\).
Suy ra \[BC = \sqrt {289,25} \approx 17\,\,{\rm{(cm)}}\].
Vì \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\) nên chiếc điện thoại theo hình vẽ là: \(\frac{{17}}{{2,54}} \approx 7\,\,({\rm{inch)}}\).
Vậy chiếc điện thoại theo hình vẽ khoảng 7 inch.
Lời giải
Các trường hợp có thể xảy ra khi chọn hai tấm thẻ bất kì là:
\[\left\{ { - 2\,;\,\, - 1} \right\}\,;\,\,\left\{ { - 2\,;\,\,0} \right\}\,;\,\,\left\{ { - 2\,;\,\,3} \right\}\,;\,\,\left\{ { - 2\,;\,\,4} \right\};\left\{ { - 2;5} \right\}\];
\[\left\{ { - 1\,;\,\,0} \right\}\,;\,\,\left\{ { - 1\,;\,\,3} \right\}\,;\,\,\left\{ { - 1\,;\,\,4} \right\}\,;\,\,\left\{ { - 1\,;\,\,5} \right\}\];
\[\left\{ {0\,;\,\,3} \right\};\left\{ {0\,;\,\,4} \right\}\,;\,\,\left\{ {0\,;\,\,5} \right\}\]; \[\left\{ {3\,;\,\,4} \right\}\,;\,\,\left\{ {3\,;\,\,5} \right\}\,;\,\,\left\{ {4;5} \right\}\].
Và ngược lại đổi vị trí hai số trong các cặp số trên.
Số các kết quả xảy ra khi chọn hai tấm thẻ phân biệt từ tập hợp đã cho là \[15 \cdot 2 = 30\].
Khi tích của hai số đã chọn bằng 0 thì số hạng đầu tiên bằng 0 hoặc số hạng thứ 2 bằng 0, ta có 10 trường hợp như thế.
Vậy xác xuất cần tìm là \[\frac{{10}}{{30}} = \frac{1}{3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.