Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:

 

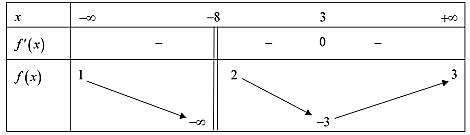
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

Đáp án B

Hướng dẫn giải

Ta có \(f'\left( x \right) = 2{\rm{cos}}x - 1\) và \(f'\left( x \right) = 0 \Leftrightarrow x = \pm \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)\).

Khi đó với \(x \in \left[ {0;\pi } \right]\) thì \(x = \frac{\pi }{3}\).

Đáp án B

Hướng dẫn giải

- Xe ô tô dừng hẳn khi \(v\left( t \right) = 0\) hay \( - 10t + 20 = 0 \Leftrightarrow t = 2\). Vậy thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 2 giây.

- Ta có xe ô tô đang chạy với tốc độ \(65{\rm{\;km/h}} \approx 18{\rm{\;m/s}}\).

Do đó, quãng đường xe ô tô còn di chuyển được kể từ lúc đạp phanh đến khi xe dừng hẳn là:

\(s\left( 2 \right) = - {5.2^2} + 20.2 = 20\left( {\rm{m}} \right)\).