Câu hỏi:

19/08/2025 247

Cho tam giác ABC, M thuộc tam giác đó. AM, BM, CM cắt BC, CA, AB tại P, R, Q. Chứng minh:

a) MA.BC + MB.CA + MC .AB ≥ 4S_ABC

b) Xác định vị trí của M để diện tích tam giác PQR lớn nhất

Xem lời giải

Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

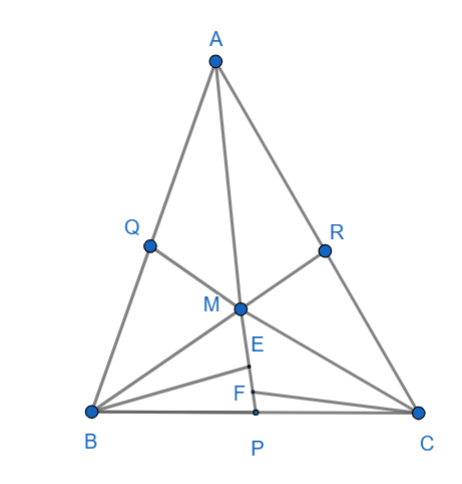
Kẻ BE, CF vuông góc với AM.

Ta có:

MA.BC = MA.(BP + CP) ≥ MA.(BE + CF) = 2S_ABM + 2S_CAM

Tương tự:

MB.CA ≥ 2S_BCM + 2S_ABM

MC.AB ≥ 2S_CAM + 2S_BCM

Suy ra:

MA.BC + MB.CA + MC.AB ≥ 2(2S_BCM + 2S_ABM + 2 S_CAM) = 4S_ABC

Dấu “=” xảy ra khi M là trực tâm

b) S_PQR = S_ABC – S_AQR – S_BPQ – S_CRQ

Đặt \(\frac{{AQ}}{{QB}} = x;\frac{{BP}}{{PC}} = y;\frac{{CR}}{{RA}} = z\)

⇒ \(\frac{{AQ}}{{AB}} = \frac{x}{{x + 1}};\frac{{AR}}{{AC}} = \frac{1}{{z + 1}}\)

\[\frac{{{S_{AQR}}}}{{{S_{ACB}}}} = \frac{{AQ}}{{AB}}.\frac{{AR}}{{AC}} = \frac{x}{{\left( {x + 1} \right)\left( {z + 1} \right)}}\]

Tương tự: \[\frac{{{S_{BPQ}}}}{{{S_{ACB}}}} = \frac{y}{{\left( {y + 1} \right)\left( {x + 1} \right)}}\]

\[\frac{{{S_{CRP}}}}{{{S_{CBA}}}} = \frac{z}{{\left( {z + 1} \right)\left( {y + 1} \right)}}\]

⇒ \[\frac{{{S_{AQR}}}}{{{S_{ACB}}}} + \frac{{{S_{BPQ}}}}{{{S_{ACB}}}} + \frac{{{S_{CRP}}}}{{{S_{CBA}}}} = \frac{z}{{\left( {z + 1} \right)\left( {y + 1} \right)}} + \frac{y}{{\left( {y + 1} \right)\left( {x + 1} \right)}} + \frac{x}{{\left( {x + 1} \right)\left( {z + 1} \right)}}\]

\[\frac{{{S_{PQR}}}}{{{S_{ABC}}}} = \frac{{xyz + 1}}{{\left( {x + 1} \right)\left( {z + 1} \right)\left( {y + 1} \right)}}\]

Theo định lý Ceva có: xyz = 1 nên

\[\frac{{{S_{PQR}}}}{{{S_{ABC}}}} = \frac{{1 + 1}}{{\left( {x + 1} \right)\left( {z + 1} \right)\left( {y + 1} \right)}} = \frac{{1 + 1}}{{1 + xy + yz + zx + x + y + z + 1}}\]

Do xy + yz + zx + x + y + z\( \ge 6\sqrt[6]{{xyz}} = 6\)

Suy ra: \[\frac{{{S_{PQR}}}}{{{S_{ABC}}}} \le \frac{2}{8} = \frac{1}{4} \Rightarrow {S_{PQR}} \le \frac{1}{4}{S_{ABC}}\]

Dấu “=” xảy ra khi M là trọng tâm.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Phân tích đa thức thành nhân tử: x⁷ + x⁵ + 1

Xem đáp án

Lời giải

Lời giải:

x⁷ + x⁵ + 1

= (x⁷ + x⁶ + x⁵) – (x⁶ – 1)

= x⁵(x² + x + 1) – (x³ – 1)(x³ + 1)

= x⁵(x² + x + 1) – (x – 1)(x² + x + 1)(x³ + 1)

= (x² + x + 1)[x⁵ – (x – 1)(x³ + 1)]

Câu 2

Giải phương trình \({x^2} - 6x + 2 = 2\left( {2 - x} \right)\sqrt {2x - 1} \)

Xem đáp án

Lời giải

Lời giải:

ĐKXĐ: \(x \ge \frac{1}{2}\)

\({x^2} - 6x + 2 = 2\left( {2 - x} \right)\sqrt {2x - 1} \)

⇔ \({x^2} + 2x\sqrt {2x - 1} + 2x - 1 = 4\left( {2x - 1} \right) + 4\sqrt {2x - 1} + 1\)

⇔ \({\left( {x + \sqrt {2x - 1} } \right)^2} = {\left( {2\sqrt {2x - 1} + 1} \right)^2}\) (*)

Do \(x \ge \frac{1}{2}\) nên \(\left\{ \begin{array}{l}x + \sqrt {2x - 1} > 0\\2\sqrt {2x - 1} + 1 > 0\end{array} \right.\)

Nên (*) tương đương: \(x + \sqrt {2x - 1} = 2\sqrt {2x - 1} + 1\)

⇔ \(x - 1 = \sqrt {2x - 1} \)

⇔ \(\left\{ \begin{array}{l}x > 1\\{\left( {x - 1} \right)^2} = 2x - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}x > 1\\x = 2 + \sqrt 2 \end{array} \right.\)

Vậy \(x = 2 + \sqrt 2 \)

Câu 3