Cho hình chữ nhật ABCD. Trên cạnh DC lấy điểm M sao cho \[DM = \frac{1}{3}DC.\] Biết AD = 15cm, AB = 24cm. Tính:
a) Chu vi hình chữ nhật ABCD.
b) Diện tích tam giác AMC.
c) Tính tỉ số phần trăm diện tích của hình tam giác ADM và hình thang ABCM.
Cho hình chữ nhật ABCD. Trên cạnh DC lấy điểm M sao cho \[DM = \frac{1}{3}DC.\] Biết AD = 15cm, AB = 24cm. Tính:
a) Chu vi hình chữ nhật ABCD.
b) Diện tích tam giác AMC.
c) Tính tỉ số phần trăm diện tích của hình tam giác ADM và hình thang ABCM.
Quảng cáo
Trả lời:
Lời giải:

a) Chu vi hình chữ nhật ABCD là:
(24 + 15) × 2 = 78 (cm2)
b) Độ dài cạnh MC là:
24 × (1 − 13) = 16 (cm)
Diện tích hình tam giác AMC là:
16 × 15 : 2=120 (cm2)
c) Độ dài cạnh DM là:
24 − 16 = 8 (cm)
Diện tích hình tam giác ADM là:
8 × 15 : 2 = 60 (cm2)
Diện tích hình thang ABCM là:
(24 + 16) × 15 : 2 = 300 (cm2)
Tỉ số phần trăm diện tích của hình tam giác ADM và hình thang ABCM là:
60 : 300 = 0,2 = 20%.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
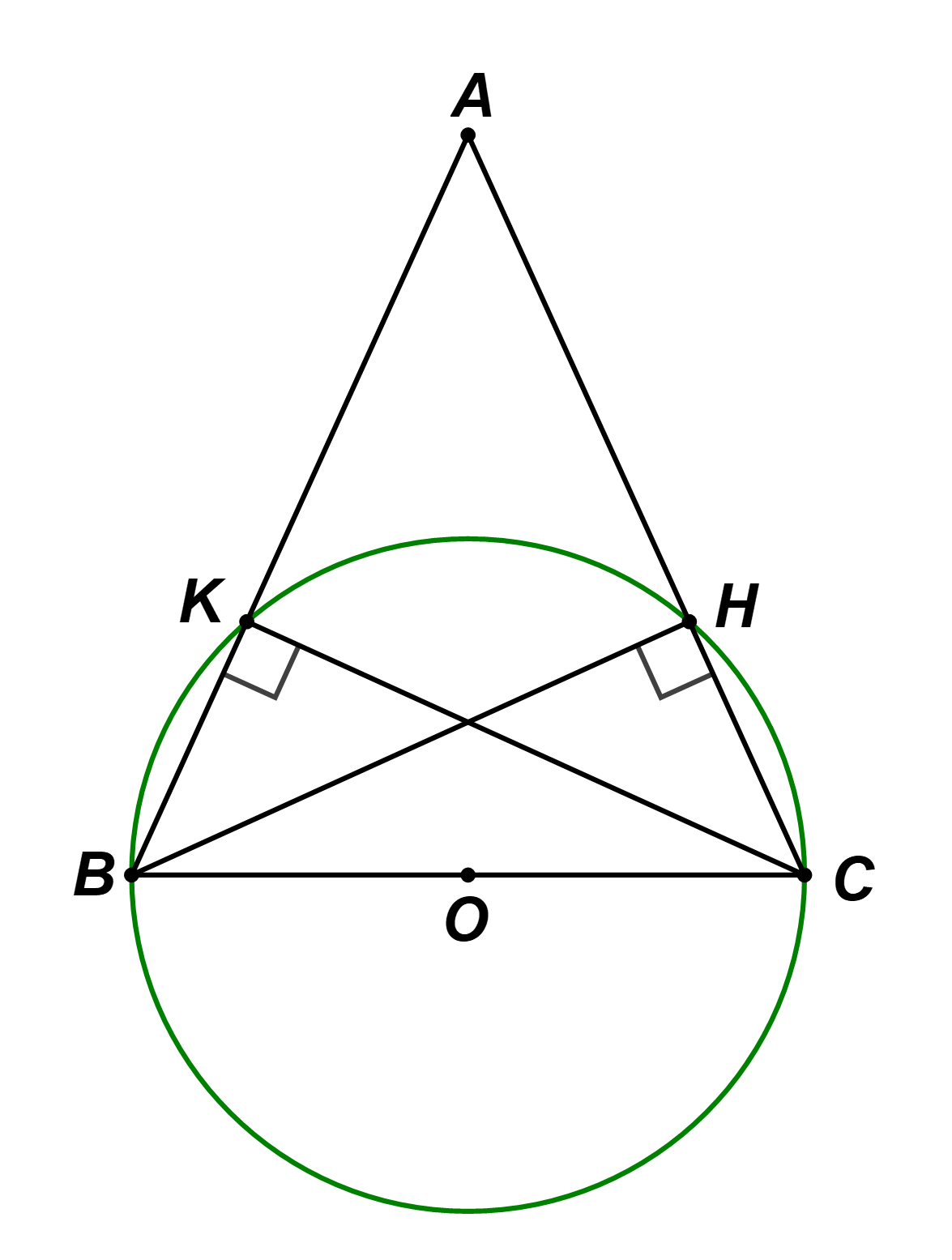
a) Vì ΔBHC vuông tại H nên H nằm trên đường tròn đường kính BC
Do đó H nằm trên (O) đường kính BC.
Vì ΔBKC vuông tại K nên K nằm trên đường tròn đường kính BC
Do đó K nằm trên (O) đường kính BC.
b) Xét ΔKBC vuông tại K và ΔHCB vuông tại H có:
BC là cạnh chung
\[\widehat {KBC} = \widehat {HCB}\] (ΔABC cân tại A)
Do đó: ΔKBC = ΔHCB (cạnh huyền – góc nhọn)
Xét (O) có:
\[\widehat {KCB}\] là góc nội tiếp chắn cung BK
\[\widehat {HBC}\] là góc nội tiếp chắn cung HC
Mà \[\widehat {KCB} = \widehat {HBC}\] nên
c) Xét ∆ABH vuông tại H, ta có: \[\widehat {ABH} + \widehat {BAH} = 90^\circ \]
Suy ra \[\widehat {ABH} = 90^\circ - \widehat {BAH} = 90^\circ - 40^\circ = 50^\circ .\]
Lại có \(\widehat {KBH}\) là góc nội tiếp chắn cung KH của đường tròn (O)Lời giải
Lời giải:
Đáp án đúng là: D
Có 6 tập con gồm 2 phần tử của A là:
{0; 3}; {0; 4}; {0; 6}; {3; 4}; {3; 6}; {4; 6}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.