Một xe đẩy xếp các thùng hàng thành một khối hàng hình hộp chữ nhật có chiều rộng là 2,4 m muốn đi qua một cái cổng hình parabol (đồ thị của hàm số (P): y = ax2 (a ≠ 0)). Biết khoảng cách giữa hai cổng là 4 m, khoảng cách từ đỉnh cổng tới mỗi chân cổng là \(2\sqrt 5 \) m (bỏ qua độ dày của cổng). Hỏi chiều cao của khối hàng không vượt quá bao nhiêu mét để có thể đi qua cổng (kết quả làm tròn đến chữ số thập phân thứ nhất)?
A. 2,4 m.
Câu hỏi trong đề: Các dạng bài tập Hàm số y = ax^2 (a ≠ 0) lớp 9 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Ta mô hình hóa bài toán trên như hình vẽ sau:
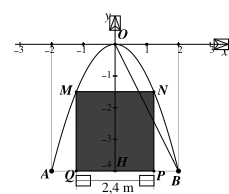
Trong đó OH = 4 m, OB = \(2\sqrt 5 \) m và MN = PQ = 2,4 m.
Khi đó, \(PH = \frac{1}{2}PQ = 1,2{\rm{\;(m)}}{\rm{.}}\)
⦁ Xét ∆OHB vuông tại H, theo định lí Pythagore, ta có:
OB2 = OH2 + HB2
Suy ra HB2 = OB2 – OH2 = \({\left( {2\sqrt 5 } \right)^2}\) – 42 = 4.
Do HB = 2 (m).
Như vậy, ta có điểm B(2; –4) thuộc parabol (P): y = ax2 (a ≠ 0).
Thay x = 2, y = –4 vào hàm số y = ax2, ta được:
–4 = a.22
–4 = a.4
a = –1 (thỏa mãn a ≠ 0).
Do đó, hàm số (P): y = –x2.
⦁ Giả sử khối hàng MNPQ khi đi qua cổng thì vừa chạm vào cổng.
Khi đó, giả sử điểm N(1,2; y0) thuộc (P).
Thay x = 1,2 và y = y0 vào hàm số y = –x2, ta được:
y0 = –(1,2)2 = –1,44.
Do đó, NP = 4 – 1,44 = 2,56 (m).
Vậy chiều cao của khối hàng không vượt quá 2,5 mét để có thể đi qua cổng (làm tròn đến chữ số thập phân thứ nhất và nếu khối hàng cao 2,6 m thì không đi qua cổng được).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
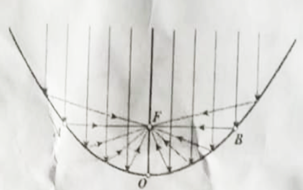
Các ăng ten parabol thu sóng hoạt động dựa theo nguyên lí: mọi tia sóng song song với trục của parabol đều có tia phản xạ đi qua tiêu điểm F của parabol (vì vậy nếu ta đặt thiết bị thu sóng tại F thì sẽ thu sóng được tốt nhất). Người ta chứng minh được rằng: Nếu đường thẳng vuông góc với trục của parabol tại F cắt parabol tại 2 điểm A, B thì \[OF = \frac{1}{4}AB\] với O là đỉnh của parabol (tham khảo hình vẽ).
Các tia sáng đều tập trung tại |
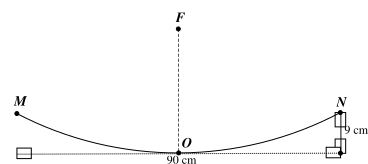
Mô hình parabol của một mặt cắt qua trục của một ăng ten parabol
Độ dài đoạn OF ứng với mô hình trên của một ăng ten parabol (ngang 90 cm và cao 9 cm) là bao nhiêu?
A. 14 m.
B. 28,125 m.
C. 56,25 m.
D. 112,5 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Do (P): y = ax2 (a ≠ 0) đi qua điểm N(45; 9) nên ta có:
Do đó 9 = a.452 hay 2025a = 9, suy ra \(a = \frac{1}{{225}}\) (thỏa mãn).
Khi đó, ta có hàm số \[y = \frac{1}{{225}}{x^2}.\]
Đường thẳng vuông góc Oy tại F cắt (P) tại A, B với xB > 0.
Ta có \[{y_B} = OF = \frac{1}{4}AB = \frac{1}{2}FB = \frac{1}{2}{x_B}.\] Khi đó, \(B\left( {{x_B};\frac{1}{2}{x_B}} \right).\)
Lại có \(B\left( {{x_B};\frac{1}{2}{x_B}} \right)\) thuộc (P) nên \[\frac{1}{2}{x_B} = \frac{1}{{225}}x_B^2.\]
Giải phương trình:
\[\frac{1}{2}{x_B} = \frac{1}{{225}}x_B^2\]
\[\frac{1}{{225}}x_B^2 - \frac{1}{2}{x_B} = 0\]
\[{x_B}\left( {\frac{1}{{225}}{x_B} - \frac{1}{2}} \right) = 0\]
xB = 0 hoặc \[\frac{1}{{225}}{x_B} - \frac{1}{2} = 0\]
xB = 0 (loại) hoặc \[{x_B} = \frac{{225}}{2}\] (thỏa mãn).
Vậy \[OF = \frac{1}{2}{x_B} = \frac{{225}}{4} = 56,25{\rm{\;(cm)}}{\rm{.}}\]
Câu 2
A. 3,3 giây.
B. 4,5 giây.
C. 5 giây.
D. 6 giây.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Khi du khách cách mặt đất 71,5 mét thì người đó đã rơi được quãng đường là:
S = 234 – 71,5 = 162,5 (m).
Thay S = 162,5 vào \(S = \frac{{13}}{2}{t^2},\) ta được:
\(162,5 = \frac{{13}}{2}{t^2},\) suy ra t2 = 25 nên t = 5 (do t > 0).
Vậy sau 5 giây thì du khách cách mặt đất 71,5 mét.
Câu 3
A. 5 giây.
B. 7 giây.
C. 9 giây.
D. 10 giây.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. F = 20v2.
B. F = 30v2.
C. 40v2.
D. 50v2.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập