Cho hình hộp chữ nhật có các kích thước như hình vẽ.

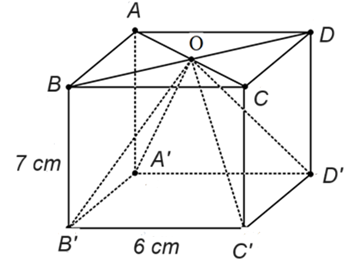
 Tính thể tích hình chóp tam giác đều \(O.A'B'C'D'\) (đơn vị: \({\rm{c}}{{\rm{m}}^{\rm{3}}}).\)

Đáp án đúng là: D

Ta có: \({\left( {x + 2} \right)^2} - 4\left( {x + 2} \right) + 4 = {\left( {x + 2 - 2} \right)^2} = {x^2}.\)

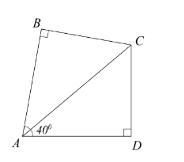
) Do \(AC\) là tia phân giác \(\widehat {BAD}\) nên ta có \(\widehat {BAD} = 2\widehat {DAC} = 2 \cdot 40^\circ  = 80^\circ \)

Xét tứ giác \(ABCD\) có: \[\widehat {BAD} + \widehat {B\,} + \widehat {BCD} + \widehat {D\,} = 360^\circ \]

Suy ra \[\widehat {BCD} = 360^\circ  - \left( {\widehat {BAD} + \widehat {B\,} + \widehat {D\,}} \right) = 360^\circ  - \left( {80^\circ  + 90^\circ  + 90^\circ } \right) = 100^\circ \].

b) Xét \(\Delta ABC\) vuông tại \(B\), theo định lí Pythagore ta có:

\(A{C^2} = A{B^2} + B{C^2} = {7,66^2} + {6,43^2} = 100,0205\)

Suy ra \(AC = \sqrt {100,0205}  \approx 10,0\) m.

Khi đó vận động viên cần bơi với vận tốc là \(\frac{{10,0}}{{20}} = 0,5\) (m/s).