B. TỰ LUẬN (3,0 điểm)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Thực hiện phép tính:
a) \(\frac{3}{5}.\frac{7}{9} + \frac{3}{5}.\frac{2}{9};\)b) \({\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 1\frac{2}{3}:\left| { - 0,75} \right| - \sqrt {\frac{1}{{16}}} \).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
a) \(\frac{3}{5}.\frac{7}{9} + \frac{3}{5}.\frac{2}{9}\) \( = \frac{3}{5}.\left( {\frac{7}{9} + \frac{2}{9}} \right)\) \( = \frac{3}{5}.1 = \frac{3}{5}.\) |
b) \({\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 1\frac{2}{3}:\left| { - 0,75} \right| - \sqrt {\frac{1}{{16}}} \) \( = {\left( { - \frac{1}{6}} \right)^2} + \frac{5}{3}:0,75 - \frac{1}{4}\) \( = \frac{1}{{36}} + \frac{5}{3}:\frac{3}{4} - \frac{1}{4}\) \( = \frac{1}{{36}} + \frac{5}{3}.\frac{4}{3} - \frac{1}{4}\) \( = \frac{1}{{36}} + \frac{{20}}{9} - \frac{1}{4}\) \( = \frac{1}{{36}} + \frac{{80}}{{36}} - \frac{9}{{36}} = \frac{{72}}{{36}} = 2\). |
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: \(45\)
• Ta có: \(\widehat {aBE} = \widehat {BED} = 60^\circ \) (giả thiết)
Mà hai góc ở vị trí so le trong.
Suy ra \(a\parallel b\).
• Ta có \(\widehat {BCD} + \widehat {BCA} = 180^\circ \) (hai góc kề bù) nên \(\widehat {BCA} = 180^\circ - \widehat {BCD} = 180^\circ - 135^\circ = 45^\circ \).
Vì \(a\parallel b\) nên \(\widehat {BCA} = \widehat {EDC}\) (hai góc đồng vị), do đó \(\widehat {CDE} = 45^\circ \).
Lời giải
Hướng dẫn giải
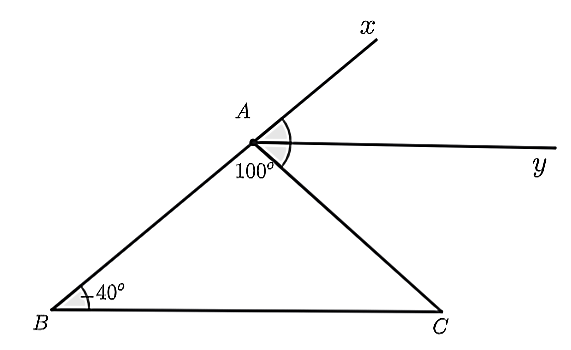
a) Ta có \(\widehat {BAC}\) và \(\widehat {CAx}\) là hai góc kề bù nên \(\widehat {BAC} + \widehat {CAx} = 180^\circ \)
Suy ra \(\widehat {xAC} = 180^\circ - \widehat {BAC} = 180^\circ - 100^\circ = 80^\circ \).
Lại có \(Ay\) là tia phân giác của \(\widehat {xAC}\) nên \(\widehat {CAy} = \widehat {yAx} = \frac{{\widehat {CAx}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \).
Suy ra \(\widehat {xAy} = \widehat {ABC} = 40^\circ \).
Mà hai góc ở vị trí đồng vị nên \(Ay\parallel BC\).
b)
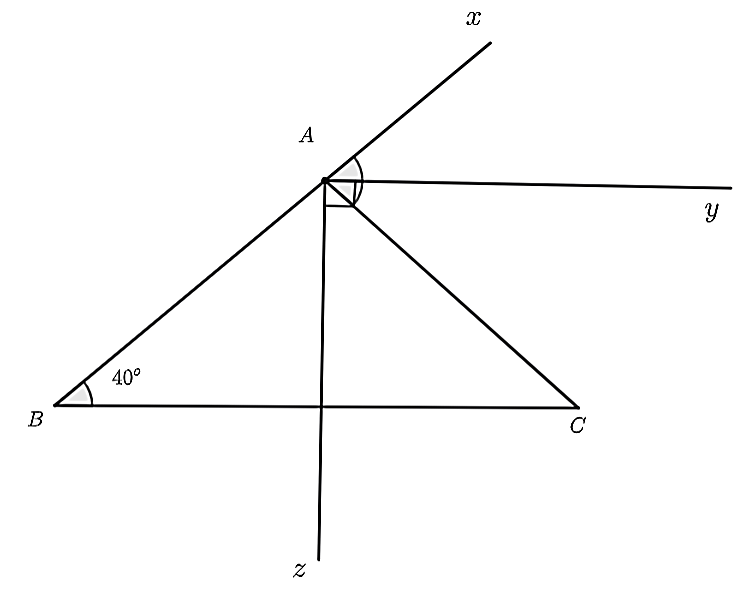
Do \(\widehat {yAC}\) và \(\widehat {zAC}\) là hai góc kề nhau nên \(\widehat {zAC} + \widehat {yAC} = \widehat {zAy}\) hay \(\widehat {zAC} + 40^\circ = 90^\circ \).
Suy ra \(\widehat {zAC} = 90^\circ - 40^\circ = 50^\circ \).
Theo đề, tia \(Az\) nằm trong \(\widehat {BAC}\) nên \(\widehat {zAC}\) và \(\widehat {zAB}\) là hai góc kề nhau (1).
Do đó, \(\widehat {zAC} + \widehat {zAB} = \widehat {BAC}\) hay \(50^\circ + \widehat {zAB} = 100^\circ \) suy ra \(\widehat {zAB} = 100^\circ - 50 = 50^\circ \).
Suy ra \(\widehat {zAC} = \widehat {zAB} = 50^\circ \) (2).
Từ (1) và (2) suy ra tia \(Az\) là tia phân giác của \(\widehat {BAC}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo