(1,0 điểm) Viện hàn lâm Nhi khoa Mỹ (AAP) khuyến nghị, khối lượng cặp sách của học sinh tiểu học và trung học cơ sở không nên vượt quá \(10\% \) khối lượng cơ thể. Một nghiên cứu tại Tây Ba Nha cũng chỉ ra, học sinh mang cặp sách nặng trong thời gian dài sẽ tăng nguy cơ mắc các bệnh về cột sống và ảnh hưởng đến chiều cao của trẻ.
Bạn Đức học lớp 7 có cân nặng \(46\) kg. Hằng ngày, bạn Đức đi học mang một chiếc cặp nặng \(3,5\) kg. Hôm nay, bạn Đức cần đem thêm một số quyển vở mới, mỗi quyển vở nặng \(\frac{{26}}{{125}}\) kg để quyên tặng học sinh vùng lũ lụt. Bạn Đức có thể mang theo nhiều nhất bao nhiêu quyển vở để khối lượng cặp sách hợp với khuyến nghị trên?
Câu hỏi trong đề: Bộ 3 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Cân nặng của chiếc cặp sách mà bạn Đức nên đeo theo khuyến nghị là: \(46.10\% = 4,6\) (kg).
Do đó, khối lượng vở mà Đức có thể mang thêm là: \(4,6 - 3,5 = 1,1\) (kg).
Suy ra số vở mà Đức có thể mang thêm là: \(1,1:\frac{{26}}{{125}} = \frac{{275}}{{52}}\) (quyển).
Ta có: \(\frac{{275}}{{52}} \approx 5,3\), mà số quyển vở là số tự nhiên. Do đó số quyển vở nhiều nhất mà Đức có thể mang là 5 quyển.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a)
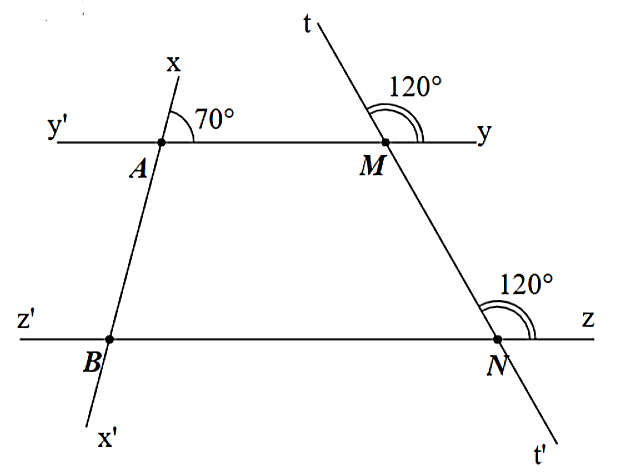
Ta có: \(\widehat {tMy} = \widehat {tNz} = 120^\circ \) và hai góc ở vị trí đồng vị nên \(yy'\parallel zz'\).
Suy ra \(\widehat {ABN} = \widehat {xAM} = 70^\circ \) (hai góc đồng vị).
Vì \(\widehat {BAM}\) và \(\widehat {xAM}\) là hai góc kề bù nên \(\widehat {BAM} + \widehat {xAM} = 180^\circ \)
Do đó \(\widehat {BAM} = 180^\circ - \widehat {xAM} = 180^\circ - 70^\circ = 110^\circ \).
Ta có \(AC\) là phân giác của \(\widehat {BAM}\) nên \(\widehat {BAC} = \widehat {CAM} = \frac{{\widehat {BAM}}}{2} = \frac{{110^\circ }}{2} = 55^\circ .\)
Vì \(yy'\parallel zz'\) nên \(\widehat {ACB} = \widehat {MAC} = 55^\circ \) (so le trong).
Lại có \(\widehat {ACB}\) và \(\widehat {ACN}\) là hai góc kề bù nên \(\widehat {ACN} + \widehat {ACB} = 180^\circ \)
Suy ra \(\widehat {ACN} = 180^\circ - \widehat {ACB} = 180^\circ - 55^\circ = 125^\circ \).
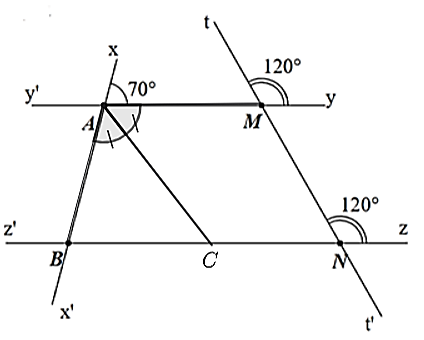
b)
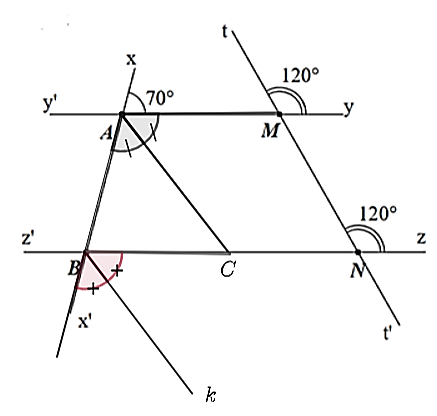
Ta có \(\widehat {ABN}\) và \(\widehat {x'BN}\) là hai góc kề bù nên \(\widehat {ABN} + \widehat {x'BN} = 180^\circ \)
Suy ra \[\widehat {x'BN} = 180^\circ - \widehat {ABN} = 180^\circ - 70^\circ = 110^\circ \].
Mà \(Bk\) là tia phân giác của \(\widehat {x'BN}\) nên \(\widehat {x'Bk} = \widehat {kBC} = \frac{{110^\circ }}{2} = 55^\circ \).
Ta có \(\widehat {x'Bk} = \widehat {BAC} = 55^\circ \) và hai góc ở vị trí đồng vị nên \(AC\parallel Bk.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng.b) Đúng.c) Đúng.d) Sai.
• Số học sinh Xuất sắc và Giỏi so với số học sinh cả lớp là \(1 - \frac{9}{{16}} = \frac{7}{{16}}\) (số học sinh).
Do đó, ý a) là đúng.
• Số học sinh Khá lớp 7A là: \(\frac{9}{{16}}.48 = 27\) (học sinh). Do đó, ý b) đúng.
• Số học sinh Giỏi và Xuất sắc của lớp 7A là: \(48 - 27 = 21\) (học sinh). Do đó, ý c) đúng.
• Ta có số học sinh Giỏi bằng \(\frac{{11}}{{10}}\) số học sinh Xuất sắc nên ta có số học sinh Giỏi là:
\(21:\left( {11 + 10} \right).11 = 11\) (học sinh).
Số học sinh Xuất sắc là: \(21 - 11 = 10\) (học sinh). Do đó, ý d) là sai.
Câu 3
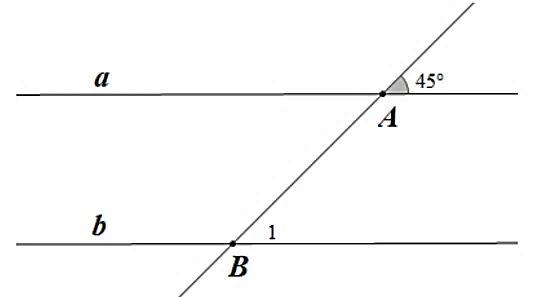
A. \(135^\circ .\)
B. \(35^\circ .\)
C. \(45^\circ .\)
D. \(145^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[x - \frac{1}{5} = \frac{3}{5}\].
B. \[x - \frac{1}{2} = \frac{3}{5}:\frac{2}{5}\].
C. \[x - \frac{2}{5} = \frac{3}{5} + \frac{1}{2}\].
D. \[x - \frac{1}{2} = \frac{3}{5} + \frac{2}{5}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
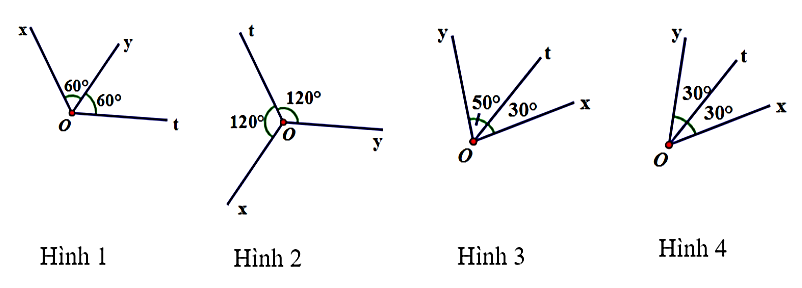
Câu 7
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.