(0,5 điểm) Sơ đồ cây gia phả 10 thế hệ của nhà bạn Thảo có đoạn trich trong hình.
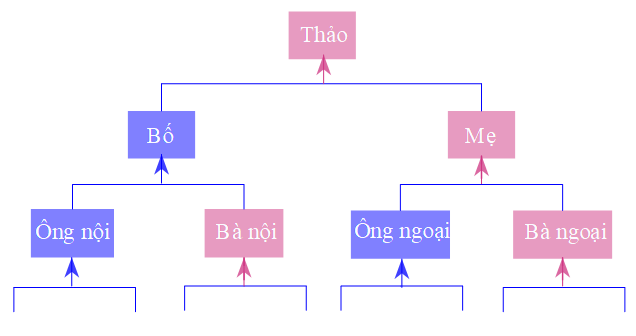
Hỏi tổng số người trong sơ đồ cây gia phả này là bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Gọi tầng cao nhất (Thảo) là tầng 1 thì số người ở tầng 1 là: \(1 = {2^0}.\)
Tầng thứ hai (Bố và Mẹ) có số người là: \(2 = {2^1}.\)
Tầng thứ ba (Ông nội, Bà nội, Ông ngoại, Bà ngoại) có số người là: \(4 = {2^2}.\)
….
Tầng thứ 10 có số người là: \({2^9}\).
Tổng số người của 10 thế hệ nhà Thảo là: \({2^0} + {2^1} + {2^2} + ... + {2^9}.\)
Đặt \(S = {2^0} + {2^1} + {2^2} + ... + {2^9}.\)
Khi đó \(2S = 2 \cdot \left( {{2^0} + {2^1} + {2^2} + ... + {2^9}} \right) = {2^1} + {2^2} + {2^3} + ... + {2^{10}}.\)
Suy ra \(2S - S = \left( {{2^1} + {2^2} + {2^3} + ... + {2^{10}}} \right) - \left( {{2^0} + {2^1} + {2^2} + ... + {2^9}} \right)\)
Do đó \(S = {2^{10}} - {2^0} = 1\,\,024 - 1 = 1\,\,023\).
Vậy tổng số người trong sơ đồ cây gia phả 10 thế hệ nhà Thảo là 1 023 người.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
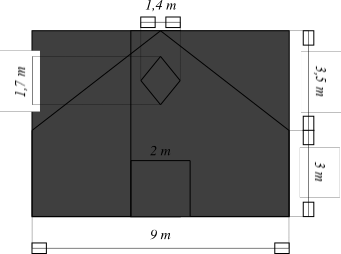
a) Công thức tính diện tích hình tam giác khi biết độ dài cạnh đáy \(a\) và chiều cao \(h\) tương ứng là:
\(\frac{1}{2}ah\) (đơn vị diện tích).
b) Diện tích cửa đi hình chữ nhật là:
Diện tích cửa thoáng hình thoi là: \(2 \cdot 2 = 4{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)\(\frac{1}{2} \cdot 1,7 \cdot 1,4 = 1,19{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
c) Diện tích của phần bức tường hình chữ nhật (không tính cửa đi) là:
\(9 \cdot 3 - 4 = 23{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích của phần bức tường hình tam giác (không tính cửa thoáng hình thoi) là:
\(\frac{1}{2} \cdot 3,5 \cdot 9 - 1,19 = 14,56{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Phần diện tích của bức tường cần sơn là:
\(23 + 14,56 = 37,56{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Số tiền bác Nam phải trả để sơn bức tường là:
\(37,56 \cdot 30\,\,000 = 1\,\,126\,\,800\) (đồng).
Lời giải
Hướng dẫn giải
|
a) \[\left( {123 - 4x} \right) - 67 = 8\] \[123 - 4x = 75\] \[4x = 48\] \(x = 12\) Vậy \(x = 12.\) b) \[\left( {3x - 1} \right) + 18 = - 40\] \[3x - 1 = - 58\] \(3x = - 57\) \(x = - 19.\) Vậy \(x = - 19.\) |
c) \(3 \cdot {\left( {2x - 11} \right)^2} + 6 = {3^4}\) \(3 \cdot {\left( {2x - 11} \right)^2} = 81 - 6\) \(3 \cdot {\left( {2x - 11} \right)^2} = 75\) \({\left( {2x - 11} \right)^2} = 25\) |
|
Trường hợp 1: \(2x - 11 = 5\) \(2x = 16\) \(x = 8\) Vậy \(x \in \left\{ {3;\,\,8} \right\}.\) |
Trường hợp 2: \(2x - 11 = - 5\) \(2x = 6\) \(x = 3\). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo