Cho hình vẽ bên, biết \(AB = DC\), \(\widehat {BAC} = \widehat {BDC} = 90^\circ \) và \(ED = 4{\rm{ cm}}\). Hỏi khoảng cách từ \(E\) đến đường thẳng \(AB\) là bao nhiêu centimet?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: \(4\)
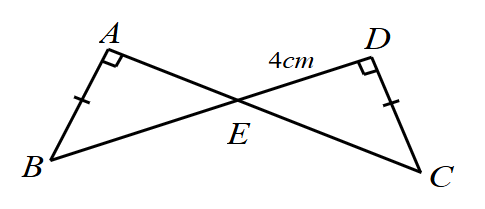
Xét
\(\Delta ABE\) có \(\widehat A + \widehat B + \widehat {AEB} = 180^\circ \) (Định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat B = 180^\circ - \widehat A - \widehat {AEB}\) (1)
Xét \(\Delta CED\) có \(\widehat C + \widehat D + \widehat {CED} = 180^\circ \) (Định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat C = 180^\circ - \widehat D - \widehat {CED}\) (2)
Mà \(\widehat {AEB} = \widehat {CED}\) (Hai góc đối đỉnh) (3)
Từ (1), (2) và (3) suy ra \(\widehat B = \widehat C\).
Xét \(\Delta ABE\) và \(\Delta DCE\) có:
\(\widehat {BAC} = \widehat {BDC} = 90^\circ \)
\(AB = CD\)
\(\widehat B = \widehat C\)
Do đó, \(\Delta ABE = \Delta DCE\) (g.c.g)
Suy ra \(AE = DE\) (hai cạnh tương ứng)
Mà \(ED = 4{\rm{ cm}}\) nên \(EA = 4{\rm{ cm}}\).
Khoảng cách từ điểm \(E\) đến đường thẳng \(AB\) là \(EA\) (Vì \(AE \bot AB\) tại \(A\))
Vậy khoảng cách từ điểm \(E\) đến đường thẳng \(AB\) là \(4{\rm{ cm}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đb) Đc) Sd) S
Gọi \(x,y,z\) lần lượt là số bút bi bác An mua loại \(I,\) \(II\), \(III\).
Điều kiện của \(x,y,z\) là \(x,y,z \in {\mathbb{N}^*}\) và \(x,y,z < 74.\)
Theo đề bài, bác An mua \(74\) chiếc bút bi nên ta có phương trình \(x + y + z = 74\).
Vì số tiền bác An mua mỗi loại bút bi là như nhau nên ta có \(6x = 5y = 4z\) hay \(\frac{x}{{\frac{1}{6}}} = \frac{y}{{\frac{1}{5}}} = \frac{z}{{\frac{1}{4}}}.\)
Theo tính chất dãy tỉ số bằng nhau nên ta có:
\(\frac{x}{{\frac{1}{6}}} = \frac{y}{{\frac{1}{5}}} = \frac{z}{{\frac{1}{4}}} = \frac{{x + y + z}}{{\frac{1}{6} + \frac{1}{5} + \frac{1}{4}}} = \frac{{74}}{{\frac{{37}}{{60}}}} = 120\).
Suy ra \(x = \frac{1}{6}.120 = 20;y = \frac{1}{5}.120 = 24;z = \frac{1}{4}.120 = 30.\)
Vậy số bút bác An mua loại \(I,\) \(II\), \(III\) lần lượt là \(20\) chiếc, \(24\) chiếc, \(30\) chiếc.
Do đó, số bút loại \(I\) ít hơn số bút loại \(II\) là \(4\) chiếc.
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đb) Đc) Đd) S
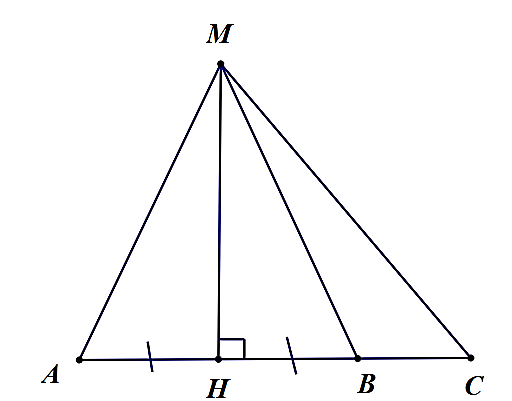
a) Vì \(MH\) là đường vuông góc và \(MA\) là đường xiên nên \(MA > MH\) (quan hệ đường vuông góc và đường xiên).
Do đó, ý a) đúng.
b) Vì \(\widehat {MBC}\) là góc ngoài của \(\Delta MHB\) suy ra \(\widehat {MBC} > \widehat {MHB} = 90^\circ \).
Xét \(\Delta MBC\) có \(\widehat {MBC}\) là góc tù nên suy ra \(MC > MB\) (quan hệ giữa góc và cạnh trong tam giác)
Do đó, ý b) đúng.
c) Mà \(HB\) và \(HC\) lần lượt là hình chiếu của \(MB\) và \(MC\) trên \(AC\).
Suy ra \(HB < HC\) (quan hệ giữa đường xiên và hình chiếu)
Vì \(AH = HB\) (gt) mà \(AH,HB\) lần lượt là hai hình chiếu của \(AM,BM\).
Suy ra \(MA = MB\) (quan hệ giữa đường xiên và hình chiếu).
Do đó, ý c) đúng.
d) Ta có \(MA = MB\) (cmt) và \(MC > MB\) (cmt) nên \(MC > MA\).
Do đó, ý d) sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.