2.1. Tính giá trị của biểu thức \(H = xy - xz + yz\) tại \(x = - 1;y = 1;z = - 1\).
2.2. Cho đa thức \(A\left( x \right) = \frac{5}{6}{x^3} - \frac{{12}}{7}{x^2} + 5x + \frac{5}{7}{x^2} + \frac{1}{6}{x^3} - 3x + 9\).
a) Thu gọn và sắp xếp đa thức \(A\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Xác định hệ số tự do của đa thức \(A\left( x \right)\) và tính \(A\left( 2 \right)\).
c) Tìm đa thức \(C\left( x \right)\) sao cho \(A\left( x \right) + C\left( x \right) = B\left( x \right)\), biết \(B\left( x \right) = {x^3} - 2{x^2} + 9x - 3\). Tìm nghiệm của đa thức \(C\left( x \right)\).
2.1. Tính giá trị của biểu thức \(H = xy - xz + yz\) tại \(x = - 1;y = 1;z = - 1\).
2.2. Cho đa thức \(A\left( x \right) = \frac{5}{6}{x^3} - \frac{{12}}{7}{x^2} + 5x + \frac{5}{7}{x^2} + \frac{1}{6}{x^3} - 3x + 9\).
a) Thu gọn và sắp xếp đa thức \(A\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Xác định hệ số tự do của đa thức \(A\left( x \right)\) và tính \(A\left( 2 \right)\).
c) Tìm đa thức \(C\left( x \right)\) sao cho \(A\left( x \right) + C\left( x \right) = B\left( x \right)\), biết \(B\left( x \right) = {x^3} - 2{x^2} + 9x - 3\). Tìm nghiệm của đa thức \(C\left( x \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
2.1. Thay \(x = - 1;y = 1;z = - 1\) vào biểu thức \(H = xy - xz + yz\), ta được:
\(H = \left( { - 1} \right).1 - \left( { - 1} \right).\left( { - 1} \right) + 1.\left( { - 1} \right) = - 1 - 1 - 1 = - 3\).
Vậy giá trị của biểu thức \(H = - 3\).
2.2. a) \(A\left( x \right) = \frac{5}{6}{x^3} - \frac{{12}}{7}{x^2} + 5x + \frac{5}{7}{x^2} + \frac{1}{6}{x^3} - 3x + 9\)
\( = \left( {\frac{5}{6} + \frac{1}{6}} \right){x^3} + \left( { - \frac{{12}}{7} + \frac{5}{7}} \right){x^2} + \left( {5 - 3} \right)x + 9\)
\( = {x^3} - {x^2} + 2x + 9\).
b) Hệ số tự do của đa thức \(A\left( x \right)\) là 9.
Ta có \(A\left( 2 \right) = {2^3} - {2^2} + 2.2 + 9 = 17\).
c) Ta có \(A\left( x \right) + C\left( x \right) = B\left( x \right)\).
Suy ra \(C\left( x \right) = B\left( x \right) - A\left( x \right)\)
\( = {x^3} - 2{x^2} + 9x - 3 - \left( {{x^3} - {x^2} + 2x + 9} \right)\)
\( = {x^3} - 2{x^2} + 9x - 3 - {x^3} + {x^2} - 2x - 9\)
\( = - {x^2} + 7x - 12\).
Để tìm nghiệm của đa thức \(C\left( x \right)\), ta cho \(C\left( x \right) = 0\)
Do đó \( - {x^2} + 7x - 12 = 0\)
\( - {x^2} + 4x + 3x - 12 = 0\)
\( - x\left( {x - 4} \right) + 3\left( {x - 4} \right) = 0\)
\(\left( { - x + 3} \right)\left( {x - 4} \right) = 0\)
Suy ra \(x = 3\) hoặc \(x = 4\).
Vậy nghiệm của đa thức \(C\left( x \right)\) là \(x \in \left\{ {3;4} \right\}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra là:
\(A = \left\{ {12;13;14;15;16;17} \right\}\).
Do đó, có 6 kết quả có thể xảy ra.
b) Kết quả thuận lợi cho biến cố \(B\) là \(12\). Do đó có 1 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố \(B\) là \(\frac{1}{6}\).
c) Kết quả thuận lợi cho biến cố \(C\) là \(14;17\). Do đó, có 2 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố \(C\) là \(\frac{2}{6} = \frac{1}{3}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
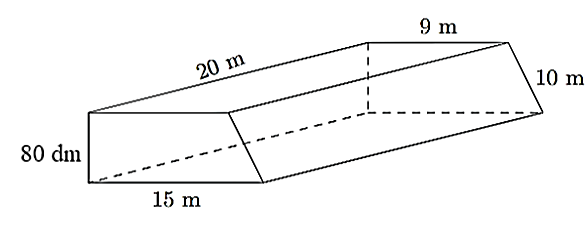
a) Đổi \(80{\rm{ dm}} = 8{\rm{ m}}\).
Thể tích của cái bục là: \(\frac{{\left( {9 + 15} \right).8}}{2}.20 = 1{\rm{ }}920{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
b) Diện tích cần phải sơn chính là diện tích toàn phần của hình lăng trụ đứng.
Diện tích xung quanh của hình lăng trụ đứng là: \(20.\left( {8 + 9 + 10 + 15} \right) = 840{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích hai đáy của lăng trụ đứng là: \(\frac{{2.\left( {9 + 15} \right).8}}{2} = 192{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích cần sơn của bục hình lăng trụ đứng này là: \(840 + 192 = 1{\rm{ }}032{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Vậy số tiền cần trả để sơn được cái bục đó là: \(1{\rm{ }}032.15{\rm{ 000}} = 15{\rm{ }}480{\rm{ }}000\) (đồng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập