1.1. Tìm \(x,\)biết:
a) \(\frac{x}{3} = \frac{{ - 10}}{6};\) b) \(\frac{{2 - x}}{4} = \frac{{x - 3}}{{ - 5}}\).
1.2. Ba đội y tế tiêm ngừa vaccine Covid – 19 tại ba trường THCS trong quận có cùng số lượng học sinh đăng kí tiêm chủng như nhau. Đội thứ nhất tiêm xong trong 5 ngày, đội thứ hai tiêm xong trong 4 ngày và đội thứ ba tiêm xong trong 6 ngày. Hỏi mỗi đội có bao nhiêu cán bộ y tế, biết cả ba đội có tất cả 37 cán bộ? (Năng suất làm việc của các cán bộ y tế là như nhau)
1.1. Tìm \(x,\)biết:
a) \(\frac{x}{3} = \frac{{ - 10}}{6};\) b) \(\frac{{2 - x}}{4} = \frac{{x - 3}}{{ - 5}}\).
1.2. Ba đội y tế tiêm ngừa vaccine Covid – 19 tại ba trường THCS trong quận có cùng số lượng học sinh đăng kí tiêm chủng như nhau. Đội thứ nhất tiêm xong trong 5 ngày, đội thứ hai tiêm xong trong 4 ngày và đội thứ ba tiêm xong trong 6 ngày. Hỏi mỗi đội có bao nhiêu cán bộ y tế, biết cả ba đội có tất cả 37 cán bộ? (Năng suất làm việc của các cán bộ y tế là như nhau)
Quảng cáo
Trả lời:
1.1.
|
a) \(\frac{x}{3} = \frac{{ - 10}}{6}\) \(6x = - 10.3\) \(6x = - 30\) \(x = - 30:6\) \(x = - 5\) Vậy \(x = - 5\). |
b) \(\frac{{2 - x}}{4} = \frac{{x - 3}}{{ - 5}}\) \( - 5\left( {2 - x} \right) = 4\left( {x - 3} \right)\) \( - 10 + 5x = 4x - 12\) \(x = - 12 + 10\) \(x = - 2\) Vậy \(x = - 2\). |
1.2. Gọi số cán bộ y tế ở đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là \(x,y,z\) (người) với \(x,y,z \in {\mathbb{N}^*}.\)
Vì cả ba đội y tế có tất cả 37 cán bộ y tế nên \(x + y + z = 37\).
Ta có: \(x\) tiêm xong trong 5 ngày, \(y\) tiêm xong trong 4 ngày, \(z\) tiêm xong trong 6 ngày.
Vì số cán bộ y tế và thời gian là hai đại lượng tỉ lệ nghịch nên ta có: \(5x = 4y = 6z\) hay \(\frac{x}{{12}} = \frac{y}{{15}} = \frac{z}{{10}}.\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{{12}} = \frac{y}{{15}} = \frac{z}{{10}} = \frac{{x + y + z}}{{12 + 15 + 10}} = \frac{{37}}{{37}} = 1\).
Do đó, ta có: \(\frac{x}{{12}} = 1\) nên \(x = 12,\) \(\frac{y}{{15}} = 1\) nên \(y = 15\); \(\frac{z}{{10}} = 1\) nên \(z = 10\).
Vậy số cán bộ y tế ở đội thứ nhất, thứ hai, thứ ba lần lượt là 12, 15, 10 người.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra là:
\(A = \left\{ {12;13;14;15;16;17} \right\}\).
Do đó, có 6 kết quả có thể xảy ra.
b) Kết quả thuận lợi cho biến cố \(B\) là \(12\). Do đó có 1 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố \(B\) là \(\frac{1}{6}\).
c) Kết quả thuận lợi cho biến cố \(C\) là \(14;17\). Do đó, có 2 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố \(C\) là \(\frac{2}{6} = \frac{1}{3}\).Lời giải
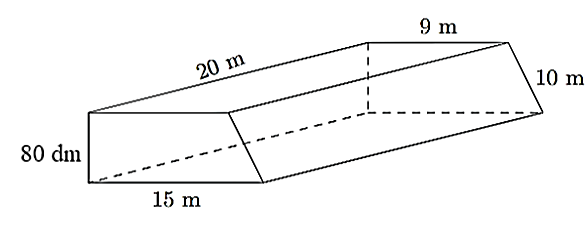
a) Đổi \(80{\rm{ dm}} = 8{\rm{ m}}\).
Thể tích của cái bục là: \(\frac{{\left( {9 + 15} \right).8}}{2}.20 = 1{\rm{ }}920{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
b) Diện tích cần phải sơn chính là diện tích toàn phần của hình lăng trụ đứng.
Diện tích xung quanh của hình lăng trụ đứng là: \(20.\left( {8 + 9 + 10 + 15} \right) = 840{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích hai đáy của lăng trụ đứng là: \(\frac{{2.\left( {9 + 15} \right).8}}{2} = 192{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích cần sơn của bục hình lăng trụ đứng này là: \(840 + 192 = 1{\rm{ }}032{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Vậy số tiền cần trả để sơn được cái bục đó là: \(1{\rm{ }}032.15{\rm{ 000}} = 15{\rm{ }}480{\rm{ }}000\) (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.