Cho tam giác \(\Delta ABC\) và \(M\) là một điểm nằm trong tam giác. Gọi \(I\) là giao điểm của đường thẳng \(BM\) và cạnh \(AC\).
a) \(MA < MI + IA.\)
b) \(MA + MB < IA + IB.\)
c) \(IA + IB < CA + CB.\)
d) \(MA + MB < CA + CB.\)
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: a) Đb) Đ c) Đd) Đ
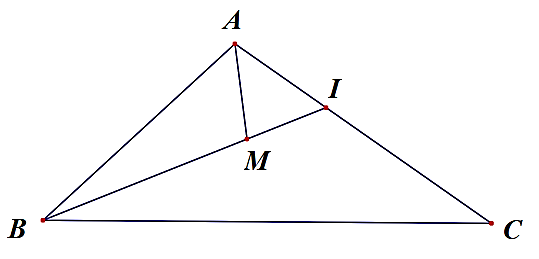
Xét
\(\Delta AMI\), theo bất đẳng thức tam giác, ta có: \(MA < MI + IA\).
Từ \(MA < MI + IA\), cộng hai vế với \(MB\), ta có:
\(MA + MB < MI + IA + MB\) hay \(MA + MB < IB + IA\).
Xét \(\Delta IBC\), theo bất đẳng thức tam giác, ta có: \(IB < BC + CI.\)
Do đó, \(IB + IA < CA + CB\).
Ta có: \(MA + MB < IB + IA\) và \(IB + IA < CA + CB\) suy ra \(MA + MB < CA + CB.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đb) Đc) Sd) Đ
Gọi \(x,y,z\) lần lượt là số mớ rau bác Cường mua gồm rau muống, rau cải và rau đay.
Điều kiện của \(x,y,z\) là \(x,y,z \in {\mathbb{N}^*}\) và \(x,y,z < 39.\)
Phương trình biểu diễn tổng số rau bác Cường mua là \(x + y + z = 39\).
Số tiền bác Cường mua mỗi loại rau là như nhau nên ta có tỉ lệ thức \(6x = 8y = 4z\) hay
\(\frac{x}{{\frac{1}{6}}} = \frac{y}{{\frac{1}{8}}} = \frac{z}{{\frac{1}{4}}}.\)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{\frac{1}{6}}} = \frac{y}{{\frac{1}{8}}} = \frac{z}{{\frac{1}{4}}} = \frac{{x + y + z}}{{\frac{1}{6} + \frac{1}{8} + \frac{1}{4}}} = \frac{{39}}{{\frac{{13}}{{24}}}} = 72\).
Suy ra \(x = \frac{1}{6}.72 = 12;y = \frac{1}{8}.72 = 9;z = \frac{1}{4}.72 = 18\).
Do đó, bác Cường mua số mớ rau muống, rau cải, rau đay lần lượt là \(12\) mớ, \(9\) mớ và \(18\) mớ.
Lời giải
Hướng dẫn giải
Đáp án: \(2\)
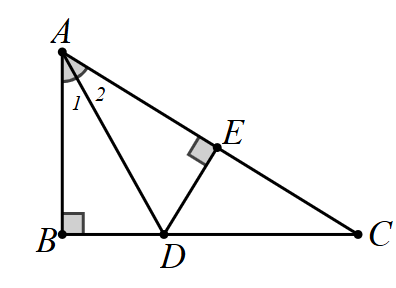
Xét
\(\Delta ABD\) và \(\Delta AED\), có:
\(\widehat B = \widehat E = 90^\circ \)(gt)
\(AD\): chung (gt)
\(\widehat {{A_1}} = \widehat {{A_2}}\) (vì \(AD\) là tia phân giác của \(\widehat {BAC}\))
Do đó, \(\Delta ABD = \Delta AED\) (g.c.g)
Suy ra \(BD = ED\) (hai cạnh tương ứng)
Mà \(BD = 2{\rm{ cm}}\) nên \(ED = 2{\rm{ cm}}{\rm{.}}\)
Vậy khoảng cách từ \(D\) đến đường thẳng \(AC\) là \(2{\rm{ cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
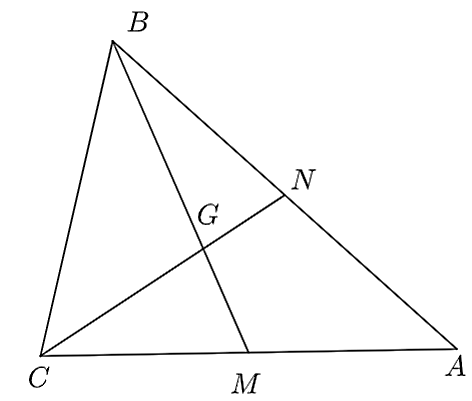
Câu 4
A. \(CG = \frac{{GN}}{2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \( - 4.\)
B. \(4.\)
C. \(16.\)
D. \( - 16.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.