Trong hình vẽ có \(xy\parallel mn\). Tia \(BC\) là tia phân giác của \(\widehat {ABn}.\) Biết \(\widehat {BAx} = 70^\circ \).
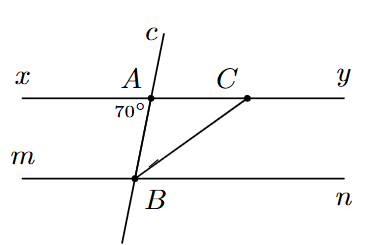
Hỏi số đo \(\widehat {ACB}\) bằng bao nhiêu độ?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: \(35\)
Vì \(xy\parallel mn\) nên \(\widehat {xAB} = \widehat {ABn} = 70^\circ \) (so le trong).
Ta có tia \(BC\) là tia phân giác của \(\widehat {ABn}\) nên \(\widehat {ABC} = \widehat {CBn} = \widehat {\frac{{ABn}}{2}} = 35^\circ \).
Vì \(xy\parallel mn\) nên \(\widehat {ACB} = \widehat {CBn} = 35^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đ b) Đ c) S d) S
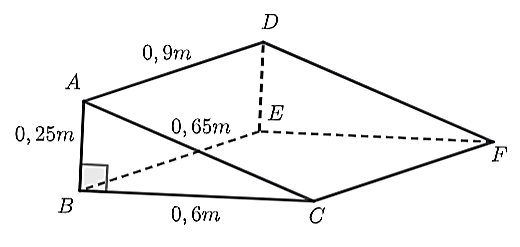
• Diện tích được quét vôi của cái gờ là: \(\left( {0,25 + 0,6 + 0,65} \right).0,9 = 1,35\) (m2).
Do đó, ý a) là đúng.
• Thể tích của cái gờ đó là: \(\frac{1}{2}.0,6.0,25.0,9 = 0,0675\) (m3)
Do đó, ý b) là đúng.
• Đổi \(0,0675{\rm{ }}{{\rm{m}}^3} = 67,5{\rm{ d}}{{\rm{m}}^3}\).
Do đó, số tiền để đổ bê tông cho cái gờ đó là: \(67,5.50{\rm{ }}000 = 3{\rm{ }}375{\rm{ }}000\) (đồng).
Do đó, ý c) là sai.
• Vậy tổng số tiền ông An phải trả là: \(3{\rm{ }}375{\rm{ }}000 + 300{\rm{ }}000 = 3{\rm{ }}675{\rm{ }}000\) (đồng).
Do đó, ý d) là sai.
Lời giải
Hướng dẫn giải
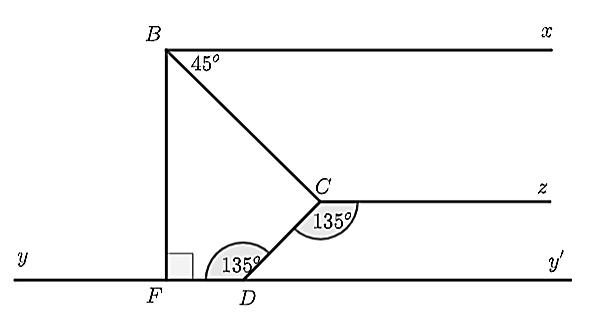
a) Nhận thấy, \(\widehat {FDC} = \widehat {DCz} = 135^\circ \) (giả thiết)
Mà hai góc ở vị trí so le trong nên \(Cz\parallel Dy.\)
b) Vì \(Dy\parallel Bx\) và \({\rm{ }}Dy \bot BF\) nên \({\rm{ }}Bx \bot BF\) tại \(B.\)
Suy ra \(\widehat {FBx} = 90^\circ \).
Nhận thấy \(\widehat {FBC}\) và \(\widehat {CBx}\) là hai góc kề nhau nên \(\widehat {FBC} + \widehat {CBx} = \widehat {FBx}\) hay \(\widehat {FBC} + 45^\circ = 90^\circ \).
Suy ra \(\widehat {FBC} = 90^\circ - 45^\circ = 45^\circ \).
Do đó, \(\widehat {FBC} = \widehat {CBx}\) và tia \(BC\) nằm giữa hai tia \(BF,Bx\) nên \(BC\) là tia phân giác của \(\widehat {FBx}.\)
c)
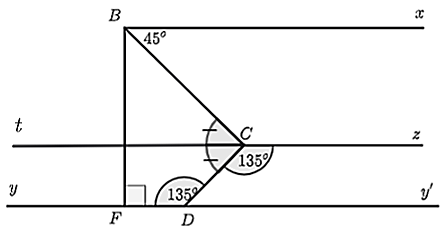
Có tia \(Ct\) là tia đối của tia \(Cz\) nên \(\widehat {tCz}\) là góc bẹt.
Có \(\widehat {tCD}\) và \(\widehat {DCz}\) là hai góc kề bù nên \(\widehat {tCD} + \widehat {DCz} = 180^\circ \) hay \(\widehat {tCD} + 135^\circ = 180^\circ \).
Suy ra \(\widehat {tCD} = 180^\circ - 135^\circ = 45^\circ \).
Vì \(Cz\parallel Dy\) và \(Dy\parallel Bx\) nên \(Cz\parallel Bx\). Do đó, \(Bx\parallel Ct\).
Suy ra \(\widehat {CBx} = \widehat {BCt} = 45^\circ \) (so le trong)
Do đó, \(\widehat {DCt} = \widehat {BCt} = 45^\circ \).
Mà \(Ct\) là tia nằm giữa hai tia \(CD\) và \(CB\).
Do đó, \(Ct\) là tia phân giác của \(\widehat {DCB}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{a}{b} = \frac{{2024}}{{2025}}.\)
B. \(\frac{{2024}}{a} = \frac{{2025}}{b}.\)
C. \(\frac{a}{{2025}} = \frac{b}{{2024}}.\)
D. \(\frac{b}{{2025}} = \frac{a}{{2024}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(8.\)
B. \(32.\)
C. \(0,5.\)
D. \(2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.