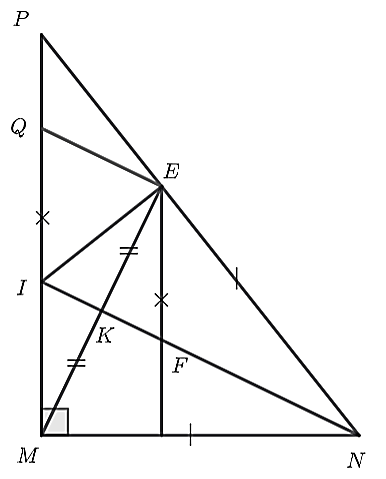
(1,5 điểm) Cho \(\Delta MNP\) vuông tại \(M\) có \(MN < MP.\) Trên cạnh \(NP\) lấy điểm \(E\) sao cho \(NM = NE.\) Gọi \(K\) là trung điểm của \(ME.\)
a) Chứng minh \(\Delta MNK = \Delta ENK.\)
b) \(NK\) cắt \(MP\) tại \(I.\) Chứng minh \(IE \bot NP.\)
c) Qua \(E\) vẽ đường thẳng song song với \(MP\) cắt \(NI\) tại \(F.\) Trên đoạn \(IP\) lấy điểm \(Q\) sao cho \(IQ = FE.\) Chứng minh \(\widehat {MNI} = \widehat {QEP}.\)
Quảng cáo
Trả lời:
Hướng dẫn giải
a) Xét \(\Delta MNK\) và \(\Delta ENK\), có:
\(MN = EN\) (gt)
\(MK = KE\) (gt)
\(KN\) chung (gt)
Do đó, \(\Delta MNK = \Delta ENK\) (c.c.c)
b) Vì \(\Delta MNK = \Delta ENK\) (cmt) nên \(\widehat {MNK} = \widehat {KNE}\) (hai góc tương ứng)
Xét \(\Delta MNI\) và \(\Delta ENI\), có:
\(MN = NE\) (gt)
\(\widehat {MNI} = \widehat {INE}\) (cmt)
\(NI\) chung (gt)
Do đó, \(\Delta MNI = \Delta ENI\) (c.g.c)
Suy ra \(\widehat {IMN} = \widehat {IEN} = 90^\circ \) (hai góc tương ứng)
Do đó, \(IE \bot PN\) tại \(E\).
c) Theo đề, ta có \(EF\parallel MP\) nên \(EF\parallel QI\).
Mà \(IQ = FE\) nên \(QEFI\) là hình bình hành.
Suy ra \(QE\parallel IF\) hay \(QE\parallel IN\).
Ta có: \(\widehat {QEP} = \widehat {INE}\) (hai góc đồng vị)
Mà \(\widehat {INE} = \widehat {INM}\) (hai góc tương ứng)
Suy ra \(\widehat {MNI} = \widehat {QEP}\) (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 (chương trình mới) ( 120.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Nhận thấy \(\left| {y + 3} \right| \ge 0\) nên \(\left| {y + 3} \right| + 5 \ge 5\) với mọi \(y.\)
\({\left( {2x - 6} \right)^2} \ge 0\) nên \({\left( {2x - 6} \right)^2} + 2 \ge 2\) với mọi \(x\).
Suy ra \(\frac{{10}}{{{{\left( {2x - 6} \right)}^2} + 2}} \le \frac{{10}}{2}\) hay \(\frac{{10}}{{{{\left( {2x - 6} \right)}^2} + 2}} \le 5\) với mọi \(x\).
Do đó, để thỏa mãn yêu cầu \(\frac{{10}}{{{{\left( {2x - 6} \right)}^2} + 2}} = \left| {y + 3} \right| + 5\) thì \(\frac{{10}}{{{{\left( {2x - 6} \right)}^2} + 2}} = \left| {y + 3} \right| + 5 = 5\).
• Giải \(\frac{{10}}{{{{\left( {2x - 6} \right)}^2} + 2}} = 5\)
\({\left( {2x - 6} \right)^2} + 2 = 10:5\)
\({\left( {2x - 6} \right)^2} + 2 = 2\)
\({\left( {2x - 6} \right)^2} = 2 - 2\)
\({\left( {2x - 6} \right)^2} = 0\)
\(2x - 6 = 0\)
\(2x = 6\)
\(x = 6:2\)
\(x = 3\).
• Giải \(\left| {y + 3} \right| + 5 = 5\).
\(\left| {y + 3} \right| = 5 - 5\)
\(\left| {y + 3} \right| = 0\)
\(y + 3 = 0\)
\(y = 0 - 3\)
\(y = - 3\).
Vậy giá trị của \(x,y\) thỏa mãn là \(x = 3\) và \(y = - 3\).
Lời giải
Hướng dẫn giải
Đáp án: \(80\)
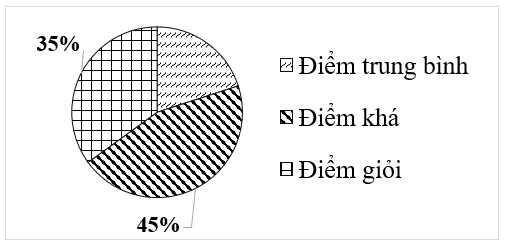
Từ biểu đồ, nhận thấy số học sinh khá chiếm \(45\% \).
Do đó, tổng số học sinh của trường THCS là: \(180:45.100 = 400\) (học sinh).
Số học sinh trung bình chiếm tỉ lệ so với số học sinh toàn trường là: \(100\% - 35\% - 45\% = 20\% \).
Do đó, số học sinh trung bình của trường đó là: \(400.20\% = 80\) (học sinh).
Câu 3
Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:
|
Loại nước uống |
Nước cam |
Nước dứa |
Nước chanh |
Nước ổi |
|
Số người chọn |
12 |
8 |
17 |
10 |
a) Nước uống được ưa chuộng nhất là nước cam.
b) Nước uống được ít người ưa chuộng nhất là nước dứa.
c) Có \(37\) người tham gia khảo sát.
d) Số người ưa chuộng nước cam và nước dứa chiếm hơn \(50\% \) trên tổng số người tham gia khảo sát.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.