Cho x, y là số hữu tỉ khác 1 thỏa mãn 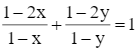 . Chứng minh M = x2 + y2 - xy là bình phương của một số hữu tỉ.
. Chứng minh M = x2 + y2 - xy là bình phương của một số hữu tỉ.
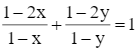 . Chứng minh M = x2 + y2 - xy là bình phương của một số hữu tỉ.
. Chứng minh M = x2 + y2 - xy là bình phương của một số hữu tỉ.Quảng cáo
Trả lời:

⇔ 
⇔ 1 – y – 2x + 2xy + 1 – x – 2y + 2xy = 1 + xy – x – y
⇔ 2x + 2y – 1 = 3xy
Khi đó: M = x2 + y2 - xy
M = (x + y)2 – 3xy
M = (x + y)2 – 2x – 2y + 1
M = (x + y)2 – 2(x + y) + 1
M = (x + y – 1)2
Vậy M = x2 + y2 - xy là bình phương của một số hữu tỉ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
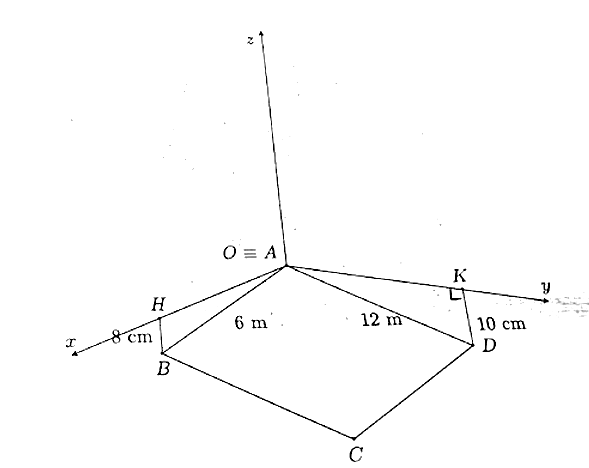
Gọi hệ trục tọa độ Oxyz như hình vẽ đã cho
O ≡ A(0;0;0)
![]()
![]()
Ta làm tròn các kết quả đến hàng đơn vị cm.
a) ![]()
⇒ Đúng
b) Sai. Tọa độ điểm D là (0;1200;-10)
c) Gọi I(xI; yI; zI) là tâm hình chữ nhật ABCD
Nên I là trung điểm BD
⇒ I(300;0;-9)
⇒ Sai
d) Ta có: ![]()
⇒ B(600;0;-8) + D(0;1200;-10) = C(xC; yC; zC)
Suy ra: C(600;1200;-18)
Nên vị trí C thấp hơn vị trí A là: |-18| = 18 (cm)
⇒ Đúng
Lời giải
a) Ta có: A = 10000000 đồng
Đặt b = 120000 đồng
Sau năm thứ nhất số tiền bác nhận được là:
A1 = A + A.3% - b = 10180000
Sau năm thứ hai số tiền bác nhận được là:
A2 = (1 + 3%)A1 – b = (1 + 3%)[(1 + 3%)A – b]
= (1 + 3%)2 A – b[(1 + (1 + 3%))
= 10365400
Sau năm thứ ba số tiền bác nhận được là:
A3 = (1 + 3%)A2 – b
= (1 + 3%)3 A – b[(1 + (1 + 3%)) + (1 + 3%)2
= 10556362
Suy ra: An = (1 + 3%)n A – b[1 + (1 + 3%)) + (1 + 3%)2 + … + (1 + 3%)n-1]

b) Từ phần a suy ra: 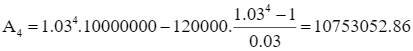 (đồng).
(đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.