Quảng cáo
Trả lời:
Giải bởi Vietjack
Giả sử tồn tại số nguyên dương n sao cho n2 + 3n + 53 ≡ 0 (mod 49)
Vì 49 chia hết cho 7 nên ta xét n2 + 3n + 53 = n2 + 3n + 49 + 4
≡ 0 (mod 7)
Nếu n = 0 thì n2 + 3n + 53 ≡ 4 (mod 7)
Nếu n = 1 thì n2 + 3n + 53 ≡ 1 (mod 7)
Nếu n = 2 thì n2 + 3n + 53 ≡ 0 (mod 7)
Nếu n = 3 thì n2 + 3n + 53 ≡ 1 (mod 7)
Nếu n = 4 thì n2 + 3n + 53 ≡ 4 (mod 7)
Nếu n = 5 thì n2 + 3n + 53 ≡ 2 (mod 7)
Nếu n = 6 thì n2 + 3n + 53 ≡ 2 (mod 7)
Thấy chỉ n = 2 thì thỏa mãn giả sử
Xét n = 7k + 2 thì n2 + 3n + 53 = 49k2 + 49k + 63 không chia hết cho 49.
Vậy giả sử ban đầu là sai.
Từ đó ta có điều phải chứng minh.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì C thuộc Ox nên C(a;0;0)
C thuộc AB nên 
cùng phương
Suy ra: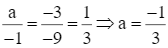 
Tức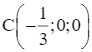 
S = 3a + b + c = -1.
Lời giải
Ta có: 
Phương trình AB là: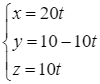 
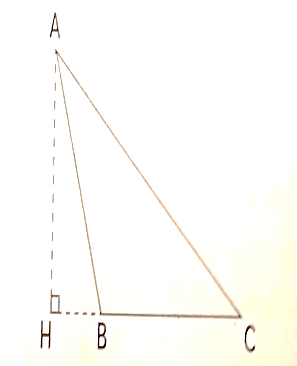
Gọi H là chân đường vuông góc của M lên AB
Mặt phẳng (P) chứa MH vuông góc với AB có phương trình:
20(x – 40) – 10(y – 10) + 10(z – 40) = 0
⇔ 2x – y + z – 110 = 0
Vì H thuộc AB nên H(20t; 10 – 10t; 10t)
Suy ra: 2.20t – 10 + 10t + 10t – 110 = 0
⇔ t = 2
Suy ra H(40;-10;20)
Vậy khoảng cách ngắn nhất từ vị trí hiện tại đến đường bay mong muốn là 20.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập