Công ty TNHH A dự định sản xuất ít nhất 80kg đường vàng và 20kg đường trắng từ hai nguyên liệu là mía và củ cải. Từ một tạ mía giá 600 ngàn đồng có thể sản xuất 40kg đường vàng và 5kg đường trắng. Từ một tạ củ cái giá 300 ngàn đồng có thể sản xuất 8kg đường vàng và 4kg đường trắng. Nhưng nhà cung cấp nguyên liệu cho công ty chỉ còn 8 tạ mía và 12 tạ củ cải. Hỏi chi phí mua nguyên liệu của công ty ít nhất là bao nhiêu ngàn đồng?
Quảng cáo
Trả lời:
Gọi x là số tạ mía sử dụng và y là số tạ củ cải sử dụng.
Chi phí mua nguyên liệu là: Z = 600x + 300y (ngàn đồng)
Mục tiêu là tìm giá trị nhỏ nhất của Z.
-
Sản lượng đường vàng: 40x + 8y ≥ 80
-
Sản lượng đường trắng: 5x + 4y ≥ 20
-
Khả năng cung cấp nguyên liệu: 0 ≤ x ≤ 8 và 0 ≤ y ≤ 12
Vẽ các đường thẳng:
-
40x + 8y = 80 ⇒ 5x + y = 10
-
5x + 4y = 20
-
x = 0
-
x = 8
-
y = 0
-
y = 12
Miền khả thi là miền nằm trên cả hai đường 40x + 8y = 80 và 5x + 4y = 20, đồng thời nằm trong hình chữ nhật giới hạn bởi x = 0, x = 8, y = 0, y = 12.
Tìm tọa độ các điểm góc của miền khả thi.
Các điểm góc của miền khả thi là: (0, 10), (0, 5), (8, 0), (8, 5), (2, 3.75), (1.6, 3.6)
Tính giá trị hàm mục tiêu tại các điểm góc.
-
Tại (0, 10): Z = 600(0) + 300(10) = 3000
-
Tại (0, 5): Z = 600(0) + 300(5) = 1500
-
Tại (8, 0): Z = 600(8) + 300(0) = 4800
-
Tại (8, 5): Z = 600(8) + 300(5) = 6300
-
Tại (2, 3.75): Z = 600(2) + 300(3.75) = 2250
-
Tại (1.6, 3.6): Z = 600(1.6) + 300(3.6) = 1800
Giá trị nhỏ nhất của Z là 1500 ngàn đồng khi x = 0 và y = 5. Tuy nhiên, điểm (0,5) không nằm trong miền khả thi. Giá trị nhỏ nhất tiếp theo là 1800 ngàn đồng tại điểm (1.6, 3.6). Tuy nhiên, ta cần kiểm tra xem điểm này có thỏa mãn điều kiện sản lượng đường không.
40(1.6) + 8(3.6) = 64 + 28.8 = 92.8 ≥ 80 (Đúng)
5(1.6) + 4(3.6) = 8 + 14.4 = 22.4 ≥ 20 (Đúng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì C thuộc Ox nên C(a;0;0)
![]()
![]()
C thuộc AB nên ![]() cùng phương
cùng phương
Suy ra: 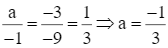
Tức 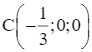
S = 3a + b + c = -1.
Lời giải
Ta có: ![]()
Phương trình AB là: 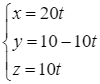
Gọi H là chân đường vuông góc của M lên AB
Mặt phẳng (P) chứa MH vuông góc với AB có phương trình:
20(x – 40) – 10(y – 10) + 10(z – 40) = 0
⇔ 2x – y + z – 110 = 0
Vì H thuộc AB nên H(20t; 10 – 10t; 10t)
Suy ra: 2.20t – 10 + 10t + 10t – 110 = 0
⇔ t = 2
Suy ra H(40;-10;20)
Vậy khoảng cách ngắn nhất từ vị trí hiện tại đến đường bay mong muốn là 20.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.