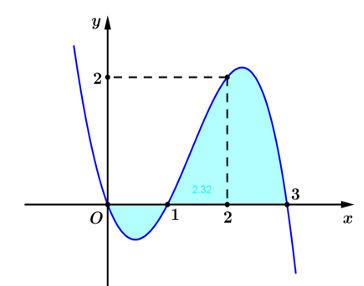
Phần hình phẳng \(\left( H \right)\) được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = {x^2} + 4x\)và hai đường thẳng \(x = - 2\;;\;x = 0\).
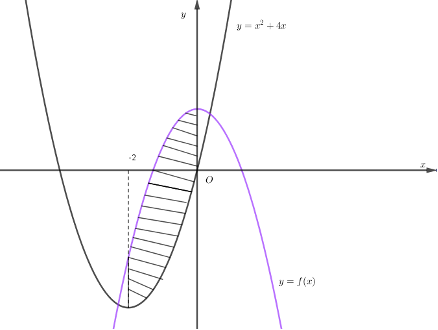
Biết \(\int\limits_{ - 2}^0 {f\left( x \right){\rm{d}}} x = \frac{4}{3}\). Tính diện tích hình \(\left( H \right)\).
Phần hình phẳng \(\left( H \right)\) được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = {x^2} + 4x\)và hai đường thẳng \(x = - 2\;;\;x = 0\).
Biết \(\int\limits_{ - 2}^0 {f\left( x \right){\rm{d}}} x = \frac{4}{3}\). Tính diện tích hình \(\left( H \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
\({S_H} = \int\limits_{ - 2}^0 {\left[ {f\left( x \right) - \left( {{x^2} + 4x} \right)} \right]} {\rm{d}}x\) \( = \int\limits_{ - 2}^0 {f\left( x \right)} {\rm{d}}x - \int\limits_{ - 2}^0 {\left( {{x^2} + 4x} \right)} {\rm{d}}x\)\( = \frac{4}{3} - \left( {\frac{{{x^3}}}{3} + 2{x^2}} \right)\left| \begin{array}{l}0\\ - 2\end{array} \right.\)\( = \frac{4}{3} + \frac{{{{\left( { - 2} \right)}^3}}}{3} + 2{\left( { - 2} \right)^2} = \frac{{20}}{3}\).
Vậy diện tích hình \(\left( H \right)\) là \(S = \frac{{20}}{3}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(S = \int\limits_{ - 1}^2 {\left[ {\frac{3}{2}x - \frac{3}{2} - \left( {\frac{1}{2}{x^4} - {x^2} - \frac{5}{2}} \right)} \right]} {\rm{d}}x = \int\limits_{ - 1}^2 {\left( { - \frac{1}{2}{x^4} + {x^2} + \frac{3}{2}x + 1} \right)} {\rm{d}}x\).
Lời giải
\(S = \int\limits_{ - 1}^3 {\left| {2x - ({x^2} - 3)} \right|dx} = \int\limits_{ - 1}^3 {\left( { - {x^2} + 2x + 3} \right)dx} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo