Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng cách \(AB = 6\;{\rm{km}}\). Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) một khoảng là \(15\;{\rm{km}}\).
Để nhận lương thực và các nhu yếu phẩm mỗi tháng người canh hải đăng phải đi xuống máy từ \(A\) đến bến tàu \(M\) trên bờ biển với vận tốc \(10\;{\rm{km/h}}\) rồi đi xe gắn máy đến \(C\) với vận tốc \(30\;{\rm{km/h}}\) (xem hình vẽ).
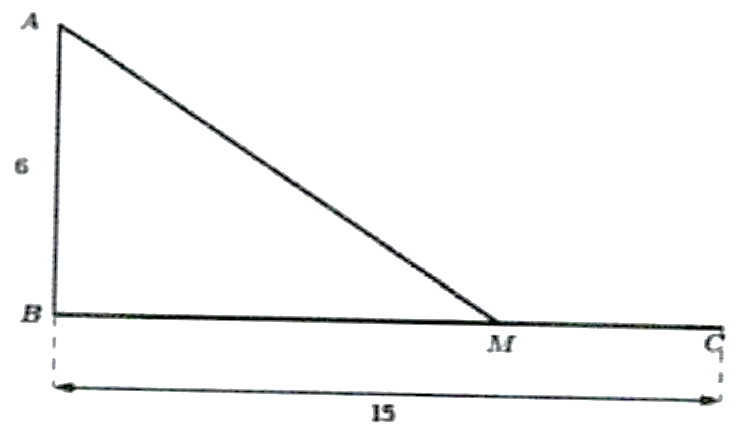
Tính tổng quãng đường người đó phải đi (đơn vị: km) biết rằng thời gian đi từ \(A\) đến \(C\) là 1 giờ 14 phút.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Ta có 1 giờ 14 phút \( = \frac{{37}}{{30}}\) giờ. Gọi \[AM = x\;\,{\rm{(km)}}\,\,\,\left( {x > 6} \right)\].
Suy ra thời gian đi từ \(A\) đến \(M\) là \(\frac{x}{{10}}\) (giờ).
Khi đó \(BM = \sqrt {{x^2} - 36} \) và \(CM = 15 - \sqrt {{x^2} - 36} \).
Thời gian đi từ \(M\) đến \(C\) là \(\frac{{15 - \sqrt {{x^2} - 36} }}{{30}}\).
Theo giả thiết ta có phương trình: \(\frac{x}{{10}} + \frac{{15 - \sqrt {{x^2} - 36} }}{{30}} = \frac{{37}}{{30}}\).
Giải phương trình ta được \(x = 10\,\,{\rm{(km)}}\).
Do đó tổng quảng đường phải đi là \(AM + MC = 10 + \left( {15 - \sqrt {{{10}^2} - 36} } \right) = 17\,\,{\rm{(km)}}\).
Đáp án: 17.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
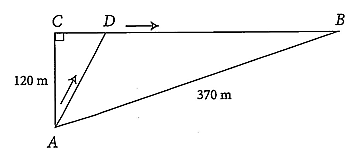
Gọi thời gian chú thỏ chạy trên đoạn \(AD\) là \(x\,\,\left( {0 < x < 30} \right)\) (giây), khi đó thời gian chú thỏ chạy trên đoạn \(BD\) là \(30 - x\) (giây). Do đó, quãng đường \(AD\) và \(BD\) lần lượt là \(13x\,\,{\rm{(m)}}\) và \(15\left( {30 - x} \right)\,\,{\rm{(m)}}\).
Độ dài quãng đường \(BC\) là: \(\sqrt {{{370}^2} - {{120}^2}} = 350\,\,{\rm{(m)}}\).
Tam giác \(ACD\) vuông tại \(C\) nên \(CD = \sqrt {{{\left( {13x} \right)}^2} - {{120}^2}} \,\,{\rm{(m)}}\).
Mặt khác, \(CD = BC - BD = 350 - 15\left( {30 - x} \right)\,\,{\rm{(m)}}\).
Do đó, ta có: \(\sqrt {{{\left( {13x} \right)}^2} - {{120}^2}} = 350 - 15\left( {30 - x} \right)\).
Giải phương trình này và kết hợp với điều kiện \(0 < x < 30\), ta nhận \(x = 10\) (giây).
Vậy khoảng cách giữa vị trí \(C\) và vị trí \(D\) là: \(350 - 15 \cdot \left( {30 - 10} \right) = 50\,\,{\rm{(m)}}\).
Đáp án: \(50\).
Lời giải
Lời giải
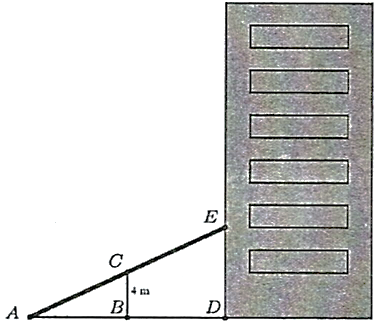
Đặt \(AB = x > 0\). Xét tam giác \(ABC\) vuông tại \(B\) có: \(AC = \sqrt {{x^2} + 4} \).
Theo tính chất định lí Thalès, ta có: \(\frac{{AC}}{{AB}} = \frac{{CE}}{{BD}} \Leftrightarrow \frac{{\sqrt {{x^2} + 16} }}{x} = \frac{5}{3}\)
\( \Leftrightarrow 3\sqrt {{x^2} + 16} = 5x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}5x \ge 0\\9\left( {{x^2} + 16} \right) = 25{x^2}\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge 0\\16{x^2} = 144\end{array}\end{array} \Leftrightarrow x = 3.} \right.} \right.\)
Vậy hai vị trí \(A,B\) cách nhau \(3\;{\rm{m}}\).
Đáp án: \(3\;\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo