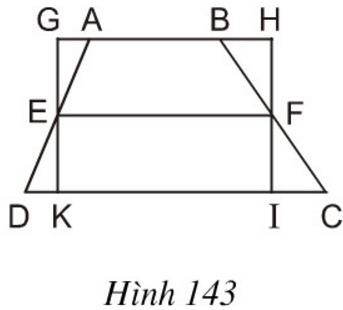
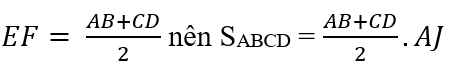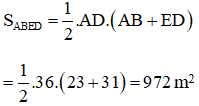Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.
Câu hỏi trong đề: Giải toán 8: Chương 2: Đa giác. Diện tích đa giác !!
Quảng cáo
Trả lời:
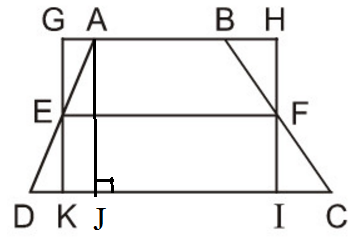
Ta có hình thang ABCD (AB // CD) với đường trung bình EF và hình chữ nhật GHIK như hình vẽ.
Dễ dàng chứng minh:
ΔAEG = ΔDEK, ΔBFH = ΔCFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên SABCD = SGHIK
Mà SGHIK = GH.GK= EF. AJ ( vì GH = EF, GK = AJ)
Nên SABCD = EF. AJ
Lại có:
Vậy ta gặp lại công thức tính diện tích hình thang đã học nhưng bằng một phương pháp chứng minh khác.
Mặt khác, ta phát hiện công thức mới: Diện tích hình thang bằng tích của đường trung bình hình thang với đường cao.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
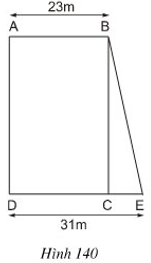
Ta có: SABCD = 828m2
⇔ AD.AB = 828
Mà AB = 23m ⇒ AD = 36m.
Diện tích hình thang ABED là:
Lời giải
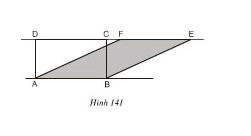
Hình chữ nhật ABCD và hình bình hành ABEF có đáy chung là AB và có chiều cao bằng nhau, vậy chúng có diện tích bằng nhau.
Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước:
- Lấy một cạnh của hình bình hành ABEF làm một cạnh của hình chữ nhật cần vẽ, chẳng hạn cạnh AB.
- Vẽ đường thẳng EF.
- Từ A và B vẽ các đường thẳng vuông góc với đường thẳng EF chúng cắt đường thẳng EF lần lượt tại D, C. Vẽ các đoạn thẳng AD, BC.
ABCD là hình chữ nhật có cùng diện tích với hình bình hành ABEF đã cho.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.