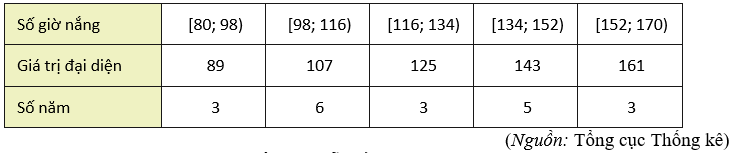
Một vận động viên luyện tập chạy cự li 100 m đã ghi lại kết quả luyện tập như sau:

Tìm phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm này. Phương sai và độ lệch chuẩn cho biết điều gì?

Xem lời giải

Câu hỏi trong đề: (Trả lời ngắn) 20 bài tập Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn giá trị đại diện cho mẫu số liệu ta có:

(Trả lời ngắn) Một vận động viên luyện tập chạy cự li 100 m đã ghi lại kết quả luyện tập như sau: (ảnh 2)

Tống số vận động viền là: \(3 + 7 + 8 + 2 = 20\).

Thời gian chạy trung bình là: \(\frac{{10,3.3 + 10,5.7 + 10,7.8 + 10,9.2}}{{20}} = 10,59\).

Phương sai của mẫu số liệu là

\({s^2} = \frac{{{{10,3}^2} \cdot 3 + {{10,5}^2} \cdot 7 + {{10,7}^2} \cdot 8 + {{10,9}^2} \cdot 2}}{{20}} - {10,59^2} = 0,0299.{\rm{ }}\)

Độ lệch chuấn của mẫu số liệu là: \(s = \sqrt {0,0299} \approx 0,17\).

Dựa vào phương sai và độ lệch chuấn ta có kết luận rằng mẫu số liệu kết quả luyện tập có tính đồng đều, dư liệu có xu hướng gần giá trị trung bình và ít bị phân tán.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Người ta theo dõi sự thay đổi cân nặng, được tính bằng hiệu cân nặng trước và sau ba tháng áp dụng chế độ ăn kiêng của một số người cho kết quả như bảng dưới đây:

Tính số trung bình, phương sai, độ lệch chuẩn và nhận xét về sự thay đổi cân nặng của người nam và người nữ sau ba tháng áp dụng chế độ ăn kiêng

Xem đáp án

Lời giải

Chọn giá trị đại diện cho các nhóm số liệu, ta có:

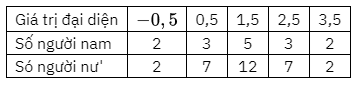
(Trả lời ngắn) Người ta theo dõi sự thay đổi cân nặng, được tính bằng hiệu cân nặng trước và sau ba tháng áp dụng chế độ ăn kiêng (ảnh 2)

Tổng số người nam là: \({n_1} = 2 + 3 + 5 + 3 + 2 = 15\).

Tổng số người nữ là: \({n_2} = 2 + 7 + 12 + 7 + 2 = 30\).

Thay đổi cân nặng trung bình của người nam là:

\({\bar x_1} = \frac{1}{{15}}[2 \cdot ( - 0,5) + 3 \cdot 0,5 + 5 \cdot 1,5 + 3 \cdot 2,5 + 2 \cdot 3,5] = 1,5(\;{\rm{kg}})\)

Thay đổi cân nặng trung bình của người nữ là:

\({\bar x_2} = \frac{1}{{30}}[2 \cdot ( - 0,5) + 7 \cdot 0,5 + 12 \cdot 1,5 + 7 \cdot 2,5 + 2 \cdot 3,5] = 1,5(\;{\rm{kg}})\)

Phương sai và độ lệch chuẩn của mẫu số liệu về thay đổi cân nặng của người nam là:

\(s_1^2 = \frac{1}{{15}}\left[ {2 \cdot {{( - 0,5)}^2} + 3 \cdot {{0,5}^2} + 5 \cdot {{1,5}^2} + 3 \cdot {{2,5}^2} + 2 \cdot {{3,5}^2}} \right] - {1,5^2} \approx {1,21^2};{s_1} \approx 1,21\)

Phương sai và độ lệch chuẩn của mẫu số liệu về thay đồi cân nặng của người nừ là:

\(s_2^2 = \frac{1}{{30}}\left[ {2 \cdot {{( - 0,5)}^2} + 7 \cdot {{0,5}^2} + 12 \cdot {{1,5}^2} + 7 \cdot {{2,5}^2} + 2 \cdot {{3,5}^2}} \right] - {1,5^2} \approx {2,06^2};{s_2} \approx 2,06.\)

Như vậy, sau ba tháng áp dụng chế độ ăn kiêng này, về trung bình sự thay đổi cân nặng của nam và nữ là như nhau. Tuy nhiên, sự biến động về thay đổi cân nặng của nữ nhiều hơn so với của nam.

Câu 2