Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh \(X\) của hai loại thuốc M và N . Công ty đã tiến hành thử nghiệm với 4000 bệnh nhân mắc bệnh X trong đó 2400 bệnh nhân dùng thuốc \({\rm{M}},1600\) bệnh nhân còn lại dùng thuốc N . Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau:
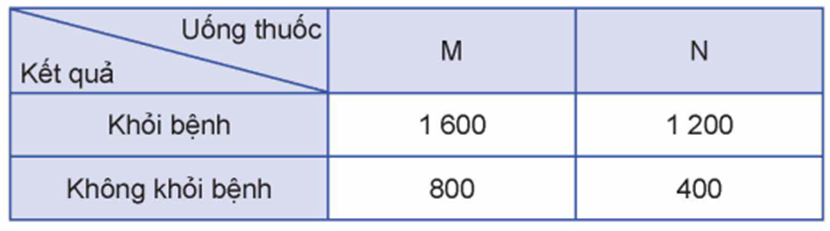
Chọn ngẫu nhiên một bệnh nhân trong số 4000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó
Quảng cáo
Trả lời:
Không gian mẫu \(\Omega \) là tập hợp 4000 bệnh nhân.
Ta có \(\bar B\) là biến cố: "Bệnh nhân đó không khỏi bệnh" và \(\bar A\) là biến cố: "Bệnh nhân đó uống thuốc \({{\rm{N}}^{\prime \prime }}\).
Ta cần tính \(P(\bar A\mid \bar B)\).
Ta có \(\bar B\) là tập hợp con của không gian mẫu gồm các bệnh nhân không khỏi bệnh. Vậy \(n(\bar B) = 800 + 400 = 1200\).
\(\bar A\bar B\) là biến cố: "Bệnh nhân đó uống thuốc N và không khỏi bệnh", \(\bar A\bar B\) là tập hợp con của không gian mẫu gồm các bệnh nhân uống thuốc N và không khỏi bệnh, ta có \(n(\bar A\bar B) = 400\)
Do đó \(P(\bar A\mid \bar B) = \frac{{P(\bar A\bar B)}}{{P(\bar B)}} = \frac{{n(\bar A\bar B)}}{{n(\bar B)}} = \frac{{400}}{{1200}} = \frac{1}{3}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vi A và B là hai biến cố độc lập nên các cặp biến cố \(\bar A\) và \(B\) ; \(A\) và \(\bar B\) cũng độc lập.
Theo định nghĩa \(P(\bar A\mid B)\) là xác suất của \(\bar A\) (tức là xác suất không xuất hiện của A ) biết rằng biến cố B đã xảy ra. Vi \(\bar A,\;{\rm{B}}\) độc lập nên việc xảy ra B không ảnh hưởng tới xác suất không xuất hiện của A .
Do đó \(P(\bar A\mid B) = P(\bar A)\).
Tương tự \(P(A\mid \bar B)\) là xác suất của A biết rằng biến cố B không xảy ra. Vì \({\rm{A}},\bar B\) độc lập nên việc không xảy ra \(B\) không ảnh hưởng tới xác suất xuất hiện của A.
Do đó \(P(A\mid \bar B) = P(A)\)
Lời giải
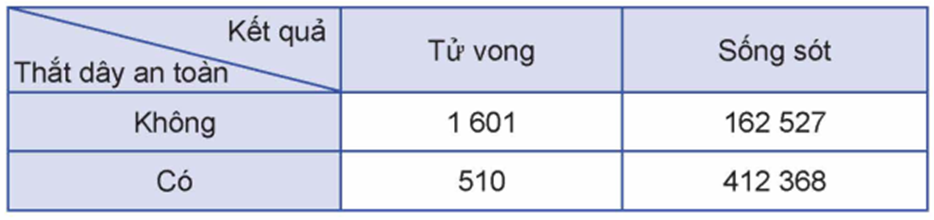
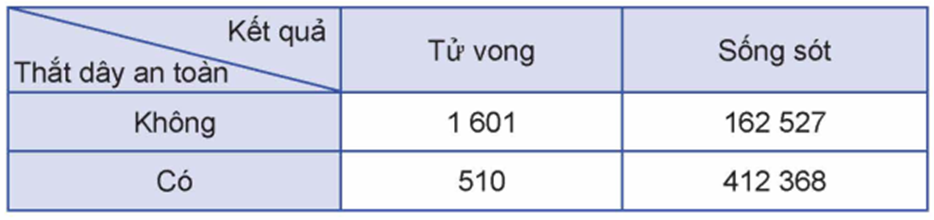
Ta có: \(\frac{{P(A\mid B)}}{{P(A\mid \bar B)}} \approx \frac{{9,755 \cdot {{10}^{ - 3}}}}{{1,235 \cdot {{10}^{ - 3}}}} \approx 7,9 \Rightarrow P(A\mid B) \approx 7,9 \cdot P(A\mid \bar B).\)
Như vậy, xác suất để một người lái xe không thắt dây an toàn bị tử vong khi xảy ra tai nạn giao thông cao gá́p khoảng 7,9 lần xác suất để một người lái xe thắt dây an toàn bị tử vong khi xảy ra tai nạn giao thông. Tức là, không thắt dây an toàn làm tăng nguy cơ bị tử vong khi xảy ra tai nạn giao thông của người lái xe lên gấp khoảng 7,9 lần.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.