Một doanh nghiệp trước khi xuất khẩu áo sơ mi trong lô hàng \(S\) phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc áo trong lô hàng đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân \(98\% \) sản phẩm làm ra qua được lần kiểm tra thứ nhất và \(95\% \) sån phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qu được lần kiểm tra thứ hai. Chọn ra ngẫu nhiên một chiếc áo sơ mi trong lô hàng . Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.
Quảng cáo
Trả lời:
Xét các biến cố:
A: "Chiếc áo sơ mi qua được lần kiểm tra thứ nhất";
\(B\) : "Chiếc áo sơ mi qua được lần kiểm tra thứ hai";
C: "Chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu".
Khi đó, xác suất để chiếc áo sơ mi qua được lần kiểm tra thứ hai, biết rằng đã qua được lần kiểm tra thứ nhất, là xác suất có điều kiện \({\rm{P}}(B\mid A)\) và \({\rm{P}}(C) = {\rm{P}}(B \cap A)\).
Ta có: \({\rm{P}}(B\mid A) = 0,95;{\rm{P}}(A) = 0,98\).
Suy ra \({\rm{P}}(C) = {\rm{P}}(B \cap A) = {\rm{P}}(A) \cdot {\rm{P}}(B\mid A) = 0,98 \cdot 0,95 = 0,931\).
Vậy xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là 0,931 .
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vi A và B là hai biến cố độc lập nên các cặp biến cố \(\bar A\) và \(B\) ; \(A\) và \(\bar B\) cũng độc lập.
Theo định nghĩa \(P(\bar A\mid B)\) là xác suất của \(\bar A\) (tức là xác suất không xuất hiện của A ) biết rằng biến cố B đã xảy ra. Vi \(\bar A,\;{\rm{B}}\) độc lập nên việc xảy ra B không ảnh hưởng tới xác suất không xuất hiện của A .
Do đó \(P(\bar A\mid B) = P(\bar A)\).
Tương tự \(P(A\mid \bar B)\) là xác suất của A biết rằng biến cố B không xảy ra. Vì \({\rm{A}},\bar B\) độc lập nên việc không xảy ra \(B\) không ảnh hưởng tới xác suất xuất hiện của A.
Do đó \(P(A\mid \bar B) = P(A)\)
Lời giải
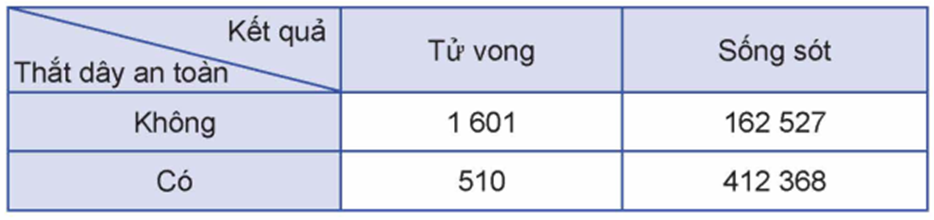
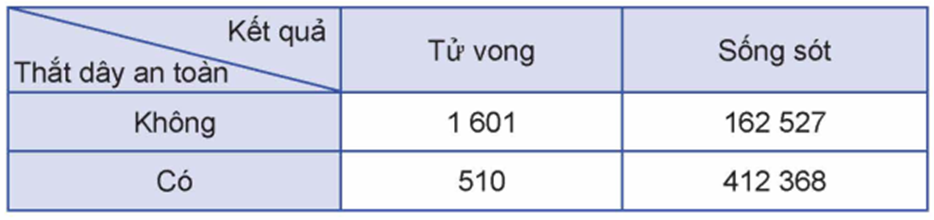
Ta có: \(\frac{{P(A\mid B)}}{{P(A\mid \bar B)}} \approx \frac{{9,755 \cdot {{10}^{ - 3}}}}{{1,235 \cdot {{10}^{ - 3}}}} \approx 7,9 \Rightarrow P(A\mid B) \approx 7,9 \cdot P(A\mid \bar B).\)
Như vậy, xác suất để một người lái xe không thắt dây an toàn bị tử vong khi xảy ra tai nạn giao thông cao gá́p khoảng 7,9 lần xác suất để một người lái xe thắt dây an toàn bị tử vong khi xảy ra tai nạn giao thông. Tức là, không thắt dây an toàn làm tăng nguy cơ bị tử vong khi xảy ra tai nạn giao thông của người lái xe lên gấp khoảng 7,9 lần.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.