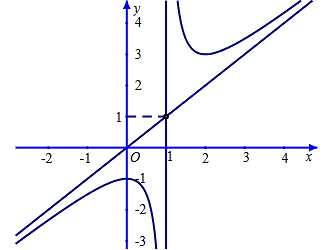
Có một chai, một vại to, một cốc, một chén và một vại nhỏ được xếp thành dãy theo thứ tự đó (tham khảo hình vẽ dưới đây), đựng các thứ nước khác nhau là: nước chè, cà phê, ca cao, sữa và bia. Nếu đem chiếc chén đặt vào giữa vật đựng chè và vật đựng sữa thì vật đựng chè và vật đựng ca cao sẽ cạnh nhau, vật đựng chè sẽ thay đổi thứ tự và vật đựng cà phê ở chính giữa.
Có một chai, một vại to, một cốc, một chén và một vại nhỏ được xếp thành dãy theo thứ tự đó (tham khảo hình vẽ dưới đây), đựng các thứ nước khác nhau là: nước chè, cà phê, ca cao, sữa và bia. Nếu đem chiếc chén đặt vào giữa vật đựng chè và vật đựng sữa thì vật đựng chè và vật đựng ca cao sẽ cạnh nhau, vật đựng chè sẽ thay đổi thứ tự và vật đựng cà phê ở chính giữa.
a) Bia được đựng trong vại to.
b) Cà phê được đựng trong chén.
c) Chè được đựng trong vại nhỏ.
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nếu đem chiếc chén đặt vào giữa vật đựng chè và vật đựng sữa thì vật đựng chè và vật đựng sữa có thể là chai và vại to hoặc vại to và cốc.
Trường hợp 1: Chén ở giữa chai và vại to
Khi đó, vại to có thể đựng chè hoặc đựng sữa. Nhưng vại to lại ở vị trí chính giữa nên nó phải đựng cà phê \( \Rightarrow \) mâu thuẫn.
Trường hợp 2: Chén ở giữa vại to và cốc.
Khi đó, chén ở vị trí chính giữa nên chén đựng cà phê nên b) đúng.
Vại to đựng chè hoặc sữa nên a) sai.
Vật đựng chè sẽ thay đổi thứ tự sau khi chuyển chén nên vật đựng chè chỉ có thể là cốc. Suy ra c) sai.
Vậy vại to đựng sữa nên d) sai.
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án:
Gọi \(x\,\,\left( {0 < x \le 14} \right)\) là số máy in cần sử dụng để in lô hàng.
Chi phí cài đặt là \(12x\).
Số giờ in hết số ấn phẩm là \(\frac{{4000}}{{30x}}\) (giờ), chi phí giám sát là \(\frac{{4000}}{{30x}} \cdot 9 = \frac{{1200}}{x}\) (USD).
Tổng chi phí in là \(P\left( x \right) = 12x + \frac{{1200}}{x}\) .
\(P'\left( x \right) = 12 - \frac{{1200}}{{{x^2}}}\)
\(P'\left( x \right) = 0 \Leftrightarrow {x^2} = 100 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = - 10\,\,\left( L \right)\end{array} \right.\).
Bảng biến thiên:
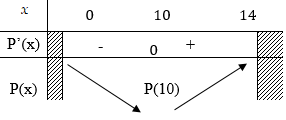
Vậy để chi phí in nhỏ nhất thì số máy phải sử dụng là \(10\) máy.
Đáp án: \(10\).
Câu 2
A. \({a^2}\).
B. \({a^2}\sqrt 2 \).
C. \( - {a^2}\).
D. \(\frac{{{a^2}\sqrt 2 }}{2}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
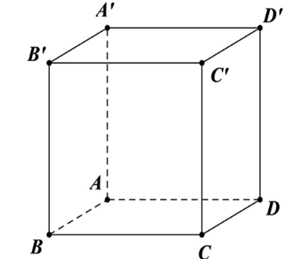
Ta có \(\overrightarrow {BC'} \cdot \overrightarrow {B'A} = \overrightarrow {AD'} \cdot \overrightarrow {B'A} = - \overrightarrow {AD'} .\overrightarrow {AB'} = - a\sqrt 2 \cdot a\sqrt 2 \cdot \cos \left( {\overrightarrow {AD'} ,\overrightarrow {AB'} } \right) = - {a^2}\). Chọn C.
Câu 3
A. \(M\left( {1;1;0} \right)\).
B. \(M\left( {3; - 4;5} \right)\).
C. \(M\left( { - 3;5;0} \right)\).
D. \(M\left( { - 2;1;0} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(M\left( {1;\,2} \right)\).
B. \(Q\left( {1;\, - 3} \right)\).
C. \(N\left( {3;\,1} \right)\).
D. \(P\left( {2;\,2} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Giá trị của biểu thức \[a + b + c + d = 0.\]
b) Hàm số đồng biến trên \[\left( { - 1;0} \right).\]
c) Gọi \[A,B\] là các điểm cực trị của đồ thị hàm số; \[M\] là điểm di động trên trục \[Ox\] sao cho \[\widehat {AMB}\] không tù. Giá trị nhỏ nhất của hoành độ điểm \[M\] là 3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
![Cho hàm số y = f( x ) liên tục và có bảng biến thiên trên đoạn [- 1;3] như hình vẽ bên.Khẳng định nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1754821452/1754821529-image5.png)
A.\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 0 \right)\).
B. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 3 \right)\).
C. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 2 \right)\).
D. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 1} \right)\) .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
a) \[\left( {SMN} \right) \bot \left( {ABCD} \right)\].
b) \[{V_{S.ABC}} = \frac{{\sqrt 3 {a^3}}}{{12}}\].
c) \[d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt 3 }}{3}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập