Phòng thí nghiệm \(B\) được giao làm hai thí nghiệm độc lập. Xác suất thành công trong từng thí nghiệm là 0,7. Phòng thành công ít nhất một thí nghiệm được coi là hoàn thành nhiệm vụ. Tính xác suất để phòng thí nghiệm \(B\) hoàn thành nhiệm vụ.
_____
Phòng thí nghiệm \(B\) được giao làm hai thí nghiệm độc lập. Xác suất thành công trong từng thí nghiệm là 0,7. Phòng thành công ít nhất một thí nghiệm được coi là hoàn thành nhiệm vụ. Tính xác suất để phòng thí nghiệm \(B\) hoàn thành nhiệm vụ.
_____
Câu hỏi trong đề: Bộ 3 đề thi KSCL đầu năm Toán 12 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \[A\] là biến cố: “thí nghiệm thứ nhất thành công”.
Gọi \(C\) là biến cố: “thí nghiệm thứ hai thành công”.
Gọi \(D\) là biến cố: “phòng thí nghiệm \(B\) thành công”.
Cách 1: Vì \(A,C\) là hai biến cố độc lập và phòng thành công ít nhất một thí nghiệm được coi là hoàn thành nhiệm vụ nên ta có: \(D = \left( {AC} \right) \cup \left( {A\overline C } \right) \cup \left( {\overline A C} \right)\). Do các biến cố \(AC;\,A\overline C ;\,\overline A C\) xung khắc nên áp dụng công thức cộng xác suất, ta có: \(P\left( D \right) = P\left( {AC} \right) + P\left( {A\overline C } \right) + P\left( {\overline A C} \right) = 0,7 \cdot 0,7 + 0,7 \cdot 0,3 + 0,3 \cdot 0,7 = 0,91\).
Cách 2: \(P\left( {\overline D } \right) = P\left( {\overline A \overline B } \right) = P\left( {\overline A } \right) \cdot P\left( {\overline B } \right) = \left( {1 - 0,7} \right) \cdot \left( {1 - 0,7} \right) = 0,09\).
Vậy \(P\left( D \right) = 1 - P\left( {\overline D } \right) = 1 - 0,09 = 0,91\).
Đáp án: \(0,91\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\,\,\left( {0 < x \le 14} \right)\) là số máy in cần sử dụng để in lô hàng.
Chi phí cài đặt là \(12x\).
Số giờ in hết số ấn phẩm là \(\frac{{4000}}{{30x}}\) (giờ), chi phí giám sát là \(\frac{{4000}}{{30x}} \cdot 9 = \frac{{1200}}{x}\) (USD).
Tổng chi phí in là \(P\left( x \right) = 12x + \frac{{1200}}{x}\) .
\(P'\left( x \right) = 12 - \frac{{1200}}{{{x^2}}}\)
\(P'\left( x \right) = 0 \Leftrightarrow {x^2} = 100 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = - 10\,\,\left( L \right)\end{array} \right.\).
Bảng biến thiên:
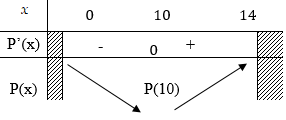
Vậy để chi phí in nhỏ nhất thì số máy phải sử dụng là \(10\) máy.
Đáp án: \(10\).
Câu 2
A. \({a^2}\).
B. \({a^2}\sqrt 2 \).
C. \( - {a^2}\).
D. \(\frac{{{a^2}\sqrt 2 }}{2}\).
Lời giải
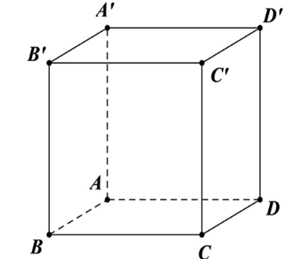
Ta có \(\overrightarrow {BC'} \cdot \overrightarrow {B'A} = \overrightarrow {AD'} \cdot \overrightarrow {B'A} = - \overrightarrow {AD'} .\overrightarrow {AB'} = - a\sqrt 2 \cdot a\sqrt 2 \cdot \cos \left( {\overrightarrow {AD'} ,\overrightarrow {AB'} } \right) = - {a^2}\). Chọn C.
Câu 3
A. \(M\left( {1;1;0} \right)\).
B. \(M\left( {3; - 4;5} \right)\).
C. \(M\left( { - 3;5;0} \right)\).
D. \(M\left( { - 2;1;0} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(M\left( {1;\,2} \right)\).
B. \(Q\left( {1;\, - 3} \right)\).
C. \(N\left( {3;\,1} \right)\).
D. \(P\left( {2;\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Giá trị của biểu thức \[a + b + c + d = 0.\]
b) Hàm số đồng biến trên \[\left( { - 1;0} \right).\]
c) Gọi \[A,B\] là các điểm cực trị của đồ thị hàm số; \[M\] là điểm di động trên trục \[Ox\] sao cho \[\widehat {AMB}\] không tù. Giá trị nhỏ nhất của hoành độ điểm \[M\] là 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
![Cho hàm số y = f( x ) liên tục và có bảng biến thiên trên đoạn [- 1;3] như hình vẽ bên.Khẳng định nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1754821452/1754821529-image5.png)
A.\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 0 \right)\).
B. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 3 \right)\).
C. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 2 \right)\).
D. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 1} \right)\) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
a) \[\left( {SMN} \right) \bot \left( {ABCD} \right)\].
b) \[{V_{S.ABC}} = \frac{{\sqrt 3 {a^3}}}{{12}}\].
c) \[d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt 3 }}{3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập