Một hộp kín đựng \[30\] tấm thẻ giống hệt nhau đánh số từ \(1\) đến \(30\). Một người rút ngẫu nhiên ra một tấm thẻ từ trong hộp. Người đó được thông báo rằng thẻ rút ra mang số chẵn. Tính xác suất để người đó rút được thẻ có số chia hết cho \(10\).
A. \(\frac{2}{5}\).
B. \(\frac{1}{5}\).
C. \(\frac{3}{{10}}\).
D. \(\frac{3}{5}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Gọi A là biến cố “Rút được thẻ có số chia hết cho \(10\)”, B là biến cố: “Rút được thẻ mang số chẵn”.
Khi đó, biến cố AB: “Rút được thẻ chẵn mang số chia hết cho \(10\)”. Suy ra:
\(n\left( {AB} \right) = 3\)\( \Rightarrow P\left( {AB} \right) = \frac{3}{{30}} = \frac{1}{{10}}\)
Có \(15\) số chẵn từ \(1\) đến \(30\)nên \(n\left( B \right) = 15\)\( \Rightarrow P\left( B \right) = \frac{{15}}{{30}} = \frac{1}{2}\)
Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{1}{5}\)
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\frac{3}{8}\].
B. \[\frac{3}{{10}}\].
C. \[\frac{2}{7}\].
D. \[\frac{1}{3}\].
Lời giải
Chọn B
Gọi A là biến cố lấy một bi xanh lần thứ nhất thì
Gọi B là biến cố lấy một bi trắng lần thứ hai.
Gọi C là biến cố lấy lần 1 một viên bi xanh, lần 2 một viên bi trắng
Nếu A đã xảy ra thì trong bình chỉ còn 2 bi xanh, 2 bi trắng. Khi đó \[P\left( {B|A} \right) = \frac{2}{4} = \frac{1}{2}\]
Mà \[C = AB\]. Do đó theo công thức nhân ta có: \[P(C) = P(AB) = P(A)P(B/A) = \frac{3}{5} \cdot \frac{1}{2} = \frac{3}{{10}}\].
Câu 2
A. \(0,16\) và \(0,24\).
B. \(0,32\) và \(0,24\).
C. \(0,24\) và \(0,36\).
D. \(0,36\) và \(0,48\).
Lời giải
Chọn C
Gọi:
- G là biến cố "Ngày có gió"
- M là biến cố "Ngày có mưa"
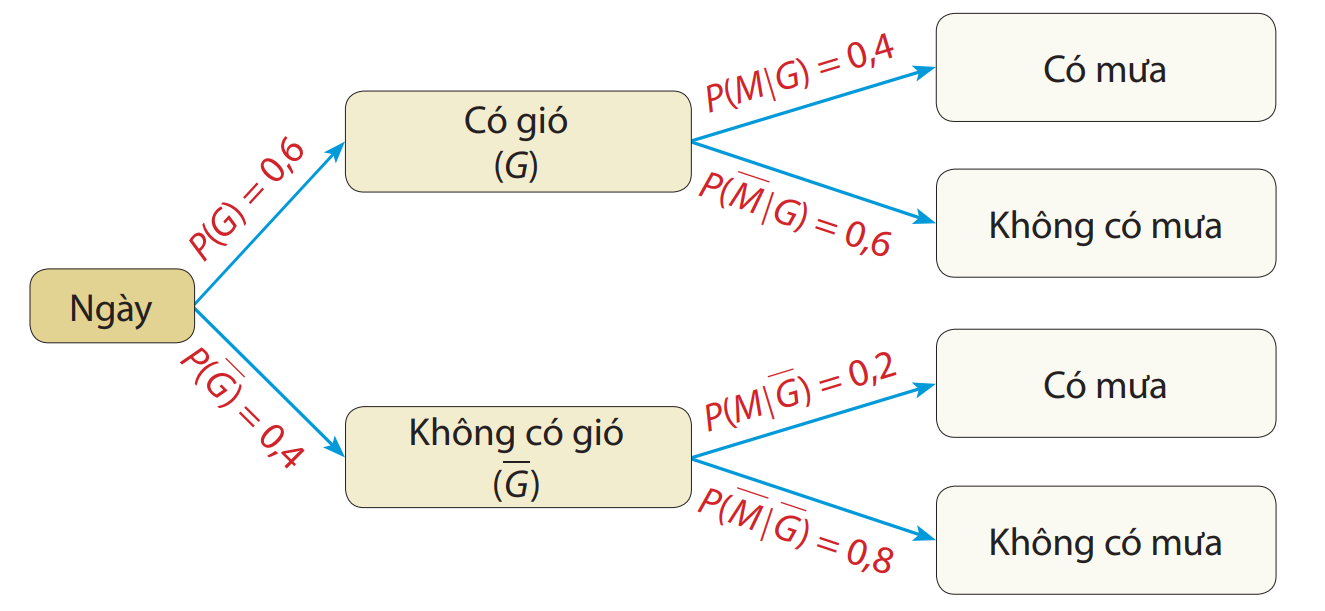
Theo đề bài, nếu ngày có gió thì xác suất có mưa là \[0,4\] nên \[P(M|G) = 0,4\].
Suy ra: \[P(M|\overline G ) = 1 - 0,4 = 0,6\].
Ngày không có gió thì xác suất có mưa là \[0,2\]nên \[P(M|\overline G ) = 0,2\].
Suy ra: \[P(\overline M |\overline G ) = 1 - 0,2 = 0,8\].
\[P(GM) = P(G){\rm{ }}.P(M|G) = 0,6{\rm{ }}.{\rm{ }}0,4{\rm{ }} = 0,24.\]
\[P(G\overline M ){\rm{ }} = P(G){\rm{ }}.P(\overline M |G) = 0,6.0,6 = 0,36.\]
Điều này có nghĩa là tại địa phương T, trong một ngày, xác suất để trời vừa có gió và vừa có mưa là \[0,24\]; xác suất để trời có gió nhưng không có mưa là \[0,36\].
Câu 3
A. \[\frac{4}{7}\].
B. \[\frac{1}{{280}}\].
C. \[\frac{1}{{190}}\].
D. \[\frac{1}{{75}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \( \approx 0,45\).
B. \( \approx 0,57\).
C. \( \approx 0,34\).
D. \( \approx 0,72\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \( \approx 0,35\).
B. \( \approx 0,29\).
C. \( \approx 0,43\).
D. \( \approx 0,32\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{1}{3}\).
B. \(\frac{3}{4}\).
C. \(1\).
D. \(\frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 0,8.
B. 0,2.
C. 0,6.
D. 0,15.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo