Cho đồ thị biến đổi trạng thái của một khối khí lí tưởng xác định từ trạng thái 1 đến trạng thái 2 như hình vẽ.

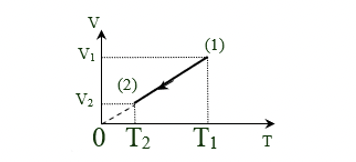
Đồ thị bên tương ứng với đồ thị biểu diễn quá trình biến đổi trạng thái của khối khí đó trong hình nào sau đây?

Hình 1                            Hình 2                                       Hình 3                                                    Hình 4

Phương pháp:

+ Nhớ lại quy ước dấu và định luật I nhiệt động lực học: \({\rm{\Delta }}U = Q + A\).

+ Công của khối khí: \(A = p.{\rm{\Delta }}V\)

Cách giải:

+ Truyền nhiệt lượng cho Q cho khối khí nén \({\rm{Q}} > 0\)

\( \to \) b sai.

+ Độ lớn công của khối khí thực hiện là:

\(\left| A \right| = p{\rm{\Delta }}V = {3.10^5}{.7.10^{ - 3}} = 2100\left( J \right)\)

\( \to \) c đúng.

Áp dụng định luật I nhiệt động lực học:

\({\rm{\Delta }}U = Q + A \Rightarrow  - 1100 = Q - 2100 \Rightarrow Q = 1000\left( J \right)\)

\( \to \) a đúng.

+ Thể tích của khối khí tăng thêm 7,0 lít

Phương pháp:

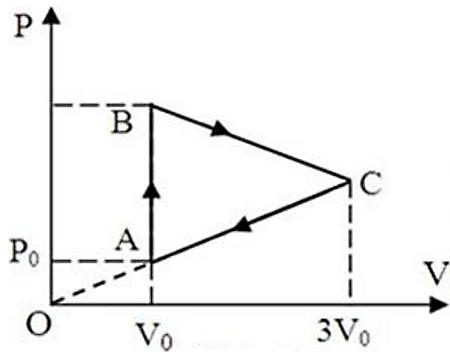
- Với \(\frac{{pV}}{T} = \) const \( \Rightarrow {T_{{\rm{max\;}}}}\) thì \({({\rm{pV}})_{{\rm{max\;}}}}\) nên trạng thái đó nằm trên đoạn BC.

- Theo đầu bài, \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\).

- Áp dụng phương trình trạng thái khí tìm \({{\rm{T}}_{{\rm{max\;}}}}\)

Cách giải:

Với \(\frac{{pV}}{T} = \)const\( \Rightarrow {T_{{\rm{max}}}}\) thì \({({\rm{pV}})_{{\rm{max}}}}\) nên trạng thái đó nằm trên đoạn BC.

Theo Talet có:

\({p_c} = 3{p_0}\) và \({T_B} = {T_C} \Rightarrow {p_B}{V_B} = {p_C}{V_C}\)

\( \Rightarrow {p_B}.{V_0} = 3{p_0}.3{V_0} \Rightarrow {p_B} = 9{p_0}\)

Ta có: \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{V = \frac{{{V_B} + {V_C}}}{2} = \frac{{{V_0} + 3{V_0}}}{2} = 2{V_0}}\\{p = \frac{{{p_B} + {p_C}}}{2} = \frac{{3{p_0} + 9{p_0}}}{2} = 6{p_0}}\end{array}} \right.\)

Phương trình trạng thái khí:

\(\frac{{pV}}{T} = \frac{{{p_0}{V_0}}}{{{T_0}}} \Rightarrow \frac{{6{p_0}2{V_0}}}{{{T_{{\rm{max}}}}}} = \frac{{{p_0}{V_0}}}{{250}}\)

\( \Rightarrow {T_{{\rm{max\;}}}} = 3000\left( {\rm{K}} \right)\)