Một ống thuỷ tinh hình trụ thẳng đứng tiết diện ngang \(S\) nhỏ, đầu trên hở, đầu dưới kín. Ống chứa một khối khí (coi là khí lí tưởng) ở trạng thái (1) có chiều cao \({\rm{L}} = 90{\rm{\;cm}}\) được ngăn cách với bên ngoài bởi một cột thuỷ ngân có độ cao \({\rm{h}} = 75{\rm{\;cm}}\), mép trên cột thuỷ ngân cách miệng trên của ống một đoạn \(l = 10{\rm{\;cm}}\). Nhiệt độ của khí trong ống là \({{\rm{t}}_0} = - {3^ \circ }{\rm{C}}\), áp suất khí quyển là \({{\rm{p}}_0} = 75{\rm{cmHg}}\).
a) Biết khối thuỷ ngân có khối lượng \({\rm{m}} = 100{\rm{\;g}}\). Lấy \({\rm{g}} = 10{\rm{\;m/}}{{\rm{s}}^2}\). Các quá trình được xem là diễn biến chậm. Công khí đã thực hiện từ trạng thái (1) đến trạng thái (2) là \(0,1{\rm{\;J}}\).
b) Nhiệt độ cần thiết cấp cho khối khí để đưa khối khí trong ống từ trạng thái (2) đến trạng thái (3) mà thuỷ ngân trong ống tràn hết ra ngoài là \({t_3} = {49,5^ \circ }{\rm{C}}\).
c) Áp suất do cột thủy ngân có độ cao \({\rm{h}}\left( {{\rm{cm}}} \right)\) gây nên cho lượng khí trong ống thủy tinh là \({{\rm{p}}_{\rm{h}}} = {\rm{mgh}}\) (cmHg).
d) Khi đưa nhiệt độ của khí trong ống đến trạng thái (2) với nhiệt độ \(t = {27^ \circ }{\rm{C}}\) thì mực trên của thuỷ ngân vừa chạm miệng ống phía trên.
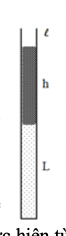
Một ống thuỷ tinh hình trụ thẳng đứng tiết diện ngang \(S\) nhỏ, đầu trên hở, đầu dưới kín. Ống chứa một khối khí (coi là khí lí tưởng) ở trạng thái (1) có chiều cao \({\rm{L}} = 90{\rm{\;cm}}\) được ngăn cách với bên ngoài bởi một cột thuỷ ngân có độ cao \({\rm{h}} = 75{\rm{\;cm}}\), mép trên cột thuỷ ngân cách miệng trên của ống một đoạn \(l = 10{\rm{\;cm}}\). Nhiệt độ của khí trong ống là \({{\rm{t}}_0} = - {3^ \circ }{\rm{C}}\), áp suất khí quyển là \({{\rm{p}}_0} = 75{\rm{cmHg}}\).
a) Biết khối thuỷ ngân có khối lượng \({\rm{m}} = 100{\rm{\;g}}\). Lấy \({\rm{g}} = 10{\rm{\;m/}}{{\rm{s}}^2}\). Các quá trình được xem là diễn biến chậm. Công khí đã thực hiện từ trạng thái (1) đến trạng thái (2) là \(0,1{\rm{\;J}}\).
b) Nhiệt độ cần thiết cấp cho khối khí để đưa khối khí trong ống từ trạng thái (2) đến trạng thái (3) mà thuỷ ngân trong ống tràn hết ra ngoài là \({t_3} = {49,5^ \circ }{\rm{C}}\).
c) Áp suất do cột thủy ngân có độ cao \({\rm{h}}\left( {{\rm{cm}}} \right)\) gây nên cho lượng khí trong ống thủy tinh là \({{\rm{p}}_{\rm{h}}} = {\rm{mgh}}\) (cmHg).
d) Khi đưa nhiệt độ của khí trong ống đến trạng thái (2) với nhiệt độ \(t = {27^ \circ }{\rm{C}}\) thì mực trên của thuỷ ngân vừa chạm miệng ống phía trên.

Quảng cáo
Trả lời:
Phương pháp:
- Công mà lượng khí thực hiện: \(A = p{\rm{\Delta }}V\).
- Áp suất do cột thủy ngân gây ra đối với lượng khí được tính bằng đơn vị cmHg thì chính bằng chiều dài của cột thủy ngân trong ống tại thời điểm xét.
- Áp dụng phương trình trạng thái khí: \(\frac{{pV}}{T} = \) const.
Cách giải:
a) Công mà khí thực hiện có độ lớn được xác định bởi: \(A = p{\rm{\Delta }}V = \rho S\ell \)
Mà \({p_h} = \frac{{mg}}{S} \Rightarrow S = \frac{{mg}}{{{p_h}}}\)
Thay vào biểu thức của A ta được:
\(A = \frac{{p.mg\ell }}{{{p_h}}} = \frac{{150.0,1.10.0,1}}{{75}} = 0,2\left( {\rm{J}} \right)\)
\( \to \) a sai.
b) Chiều dài của ống là:
\({L_0} = \ell + h + L = 10 + 75 + 90 = 175\left( {{\rm{cm}}} \right)\)
Nhiệt độ cần thiết ứng với khí có \(h' = \frac{{{L_0} - {p_0}}}{2} = \frac{{175 - 75}}{2} = 50\left( {{\rm{cm}}} \right)\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{p_3} = {p_0} + h' = 75 + 50 = 125\left( {{\rm{cmHg}}} \right)}\\{{V_3} = S.\left( {175 - 50} \right) = S.125}\\{{T_3}}\end{array}} \right.\)
Phương trình trạng thái khí lý tưởng:
\(\frac{{{p_2}{V_2}}}{{{T_2}}} = \frac{{{p_3}{V_3}}}{{{T_3}}} \Rightarrow \frac{{150.S.100}}{{300}} = \frac{{125.{\rm{S}}.125}}{{{T_3}}}\)
\( \Rightarrow {T_3} = 312,5\left( K \right) \Rightarrow {t_3} = {39,5^ \circ }{\rm{C}}\)
\( \to \) b sai.
c) Áp suất do cột thủy ngân độ cao h gây ra là \({p_h} = h\left( {{\rm{cmHg}}} \right)\)
\( \to \) c sai.
d)
Ta có:
|
p |
V |
T |
|
\({{\rm{p}}_0} + {\rm{h}} = 75 + 75 = 150\left( {{\rm{cmHg}}} \right)\) |
S.90 |
\( - 3 + 273 = 270\left( {{\rm{\;K}}} \right)\) |
|
150 cmHg |
\({\rm{S}}.\left( {90 + 10} \right) = {\rm{S}}.100\) |
\(27 + 273 = 300\left( {{\rm{\;K}}} \right)\) |
Từ (1) sang (2) là đẳng áp: \(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow \frac{{S.90}}{{270}} = \frac{{S.100}}{{300}}\) (luôn đúng)
Vậy khi đưa nhiệt độ của khí trong ống đến trạng thái (2) với nhiệt độ \(t = {27^ \circ }C\) thì mực trên của thuỷ ngân vừa chạm miệng ống phía trên.
\( \to \) d đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
+ Nhớ lại quy ước dấu và định luật I nhiệt động lực học: \({\rm{\Delta }}U = Q + A\).
+ Công của khối khí: \(A = p.{\rm{\Delta }}V\)
Cách giải:
+ Truyền nhiệt lượng cho Q cho khối khí nén \({\rm{Q}} > 0\)
\( \to \) b sai.
+ Độ lớn công của khối khí thực hiện là:
\(\left| A \right| = p{\rm{\Delta }}V = {3.10^5}{.7.10^{ - 3}} = 2100\left( J \right)\)
\( \to \) c đúng.
Áp dụng định luật I nhiệt động lực học:
\({\rm{\Delta }}U = Q + A \Rightarrow - 1100 = Q - 2100 \Rightarrow Q = 1000\left( J \right)\)
\( \to \) a đúng.
+ Thể tích của khối khí tăng thêm 7,0 lít
Lời giải
Phương pháp:
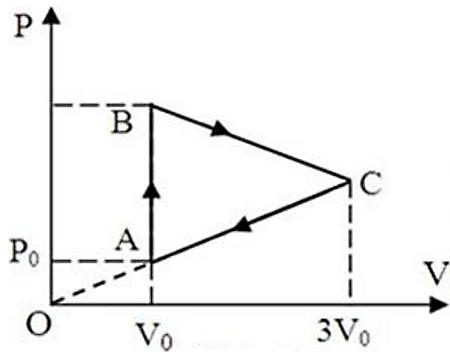
- Với \(\frac{{pV}}{T} = \) const \( \Rightarrow {T_{{\rm{max\;}}}}\) thì \({({\rm{pV}})_{{\rm{max\;}}}}\) nên trạng thái đó nằm trên đoạn BC.
- Theo đầu bài, \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\).
- Áp dụng phương trình trạng thái khí tìm \({{\rm{T}}_{{\rm{max\;}}}}\)
Cách giải:
Với \(\frac{{pV}}{T} = \)const\( \Rightarrow {T_{{\rm{max}}}}\) thì \({({\rm{pV}})_{{\rm{max}}}}\) nên trạng thái đó nằm trên đoạn BC.
Theo Talet có:
\({p_c} = 3{p_0}\) và \({T_B} = {T_C} \Rightarrow {p_B}{V_B} = {p_C}{V_C}\)
\( \Rightarrow {p_B}.{V_0} = 3{p_0}.3{V_0} \Rightarrow {p_B} = 9{p_0}\)
Ta có: \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{V = \frac{{{V_B} + {V_C}}}{2} = \frac{{{V_0} + 3{V_0}}}{2} = 2{V_0}}\\{p = \frac{{{p_B} + {p_C}}}{2} = \frac{{3{p_0} + 9{p_0}}}{2} = 6{p_0}}\end{array}} \right.\)
Phương trình trạng thái khí:
\(\frac{{pV}}{T} = \frac{{{p_0}{V_0}}}{{{T_0}}} \Rightarrow \frac{{6{p_0}2{V_0}}}{{{T_{{\rm{max}}}}}} = \frac{{{p_0}{V_0}}}{{250}}\)
\( \Rightarrow {T_{{\rm{max\;}}}} = 3000\left( {\rm{K}} \right)\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.