Một bác thợ rèn rút một con dao bằng thép khối lượng \(0,9{\rm{\;kg}}\) vừa nung xong có nhiệt độ \({750^ \circ }{\rm{C}}\) và nhúng ngay vào trong một bể nước lạnh để làm tăng độ cứng của lưỡi dao. Trong bể có 20 lít nước có nhiệt độ bằng với nhiệt độ ngoài trời là \({30^ \circ }{\rm{C}}\). Coi sự truyền nhiệt cho thành bể và môi trường xung quanh bể không đáng kể, khối lượng riêng của nước không thay đổi theo nhiệt độ. Biết nhiệt dung riêng của thép là \(460{\rm{\;J/kg}}.{\rm{K}}\), của nước là \(4200{\rm{\;J/kg}}{\rm{.K}}\) và khối lượng riêng của nước là 1 kg/lít. Nhiệt độ của nước khi có sự cân bằng nhiệt bằng bao nhiêu\({\;^ \circ }{\rm{C}}\)? (làm tròn kết quả đến chữ số hàng phần mười)
Một bác thợ rèn rút một con dao bằng thép khối lượng \(0,9{\rm{\;kg}}\) vừa nung xong có nhiệt độ \({750^ \circ }{\rm{C}}\) và nhúng ngay vào trong một bể nước lạnh để làm tăng độ cứng của lưỡi dao. Trong bể có 20 lít nước có nhiệt độ bằng với nhiệt độ ngoài trời là \({30^ \circ }{\rm{C}}\). Coi sự truyền nhiệt cho thành bể và môi trường xung quanh bể không đáng kể, khối lượng riêng của nước không thay đổi theo nhiệt độ. Biết nhiệt dung riêng của thép là \(460{\rm{\;J/kg}}.{\rm{K}}\), của nước là \(4200{\rm{\;J/kg}}{\rm{.K}}\) và khối lượng riêng của nước là 1 kg/lít. Nhiệt độ của nước khi có sự cân bằng nhiệt bằng bao nhiêu\({\;^ \circ }{\rm{C}}\)? (làm tròn kết quả đến chữ số hàng phần mười)
Quảng cáo
Trả lời:
Phương pháp:
- Tính khối lượng của nước: \(m = DV\).
- Công thức tính nhiệt độ cân bằng khi không có quá trình chuyển thể: \(t = \frac{{{m_t}{c_t}{t_t} + {m_n}{c_n}{t_n}}}{{{m_t}{c_t} + {m_n}{c_n}}}\)
Cách giải:
Khối lượng của nước: \({m_n} = {V_n}{D_n} = 20\left( {{\rm{kg}}} \right)\)
Nhiệt độ cân bằng:
\(t = \frac{{{m_t}{c_t}{t_t} + {m_n}{c_n}{t_n}}}{{{m_t}{c_t} + {m_n}{c_n}}}\)
\( \Rightarrow t = \frac{{0,9.460.750 + 20.4200.30}}{{0,9.460 + 20.4200}}\)
\( \Rightarrow t \approx {33,5^ \circ }C\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
+ Nhớ lại quy ước dấu và định luật I nhiệt động lực học: \({\rm{\Delta }}U = Q + A\).
+ Công của khối khí: \(A = p.{\rm{\Delta }}V\)
Cách giải:
+ Truyền nhiệt lượng cho Q cho khối khí nén \({\rm{Q}} > 0\)
\( \to \) b sai.
+ Độ lớn công của khối khí thực hiện là:
\(\left| A \right| = p{\rm{\Delta }}V = {3.10^5}{.7.10^{ - 3}} = 2100\left( J \right)\)
\( \to \) c đúng.
Áp dụng định luật I nhiệt động lực học:
\({\rm{\Delta }}U = Q + A \Rightarrow - 1100 = Q - 2100 \Rightarrow Q = 1000\left( J \right)\)
\( \to \) a đúng.
+ Thể tích của khối khí tăng thêm 7,0 lít
Lời giải
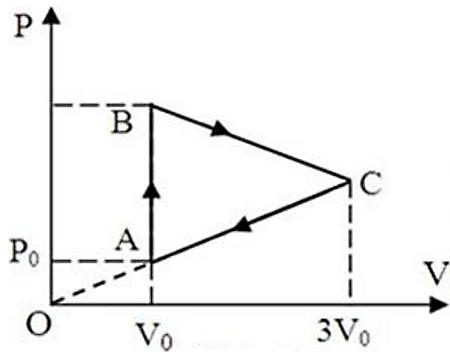
Phương pháp:
- Với \(\frac{{pV}}{T} = \) const \( \Rightarrow {T_{{\rm{max\;}}}}\) thì \({({\rm{pV}})_{{\rm{max\;}}}}\) nên trạng thái đó nằm trên đoạn BC.
- Theo đầu bài, \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\).
- Áp dụng phương trình trạng thái khí tìm \({{\rm{T}}_{{\rm{max\;}}}}\)
Cách giải:
Với \(\frac{{pV}}{T} = \)const\( \Rightarrow {T_{{\rm{max}}}}\) thì \({({\rm{pV}})_{{\rm{max}}}}\) nên trạng thái đó nằm trên đoạn BC.
Theo Talet có:
\({p_c} = 3{p_0}\) và \({T_B} = {T_C} \Rightarrow {p_B}{V_B} = {p_C}{V_C}\)
\( \Rightarrow {p_B}.{V_0} = 3{p_0}.3{V_0} \Rightarrow {p_B} = 9{p_0}\)
Ta có: \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{V = \frac{{{V_B} + {V_C}}}{2} = \frac{{{V_0} + 3{V_0}}}{2} = 2{V_0}}\\{p = \frac{{{p_B} + {p_C}}}{2} = \frac{{3{p_0} + 9{p_0}}}{2} = 6{p_0}}\end{array}} \right.\)
Phương trình trạng thái khí:
\(\frac{{pV}}{T} = \frac{{{p_0}{V_0}}}{{{T_0}}} \Rightarrow \frac{{6{p_0}2{V_0}}}{{{T_{{\rm{max}}}}}} = \frac{{{p_0}{V_0}}}{{250}}\)
\( \Rightarrow {T_{{\rm{max\;}}}} = 3000\left( {\rm{K}} \right)\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.