Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng biến thiên theo phương trình:
\({e_1} = {E_0}{\rm{cos}}\left( {\omega t} \right);{e_2} = {E_0}{\rm{cos}}\left( {\omega t - \frac{{2\pi }}{3}} \right);{e_3} = {E_0}{\rm{cos}}\left( {\omega t + \frac{{2\pi }}{3}} \right)\). Ở thời điểm mà \({{\rm{e}}_1} = 30{\rm{\;V}}\) thì \(\left| {{e_2} - {e_3}} \right| = 30{\rm{\;V}}\). Giá trị cực đại của \({{\rm{e}}_1}\) bằng bao nhiêu vôn (Kết quả làm tròn đến 1 chữ số sau dấu phẩy).
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng biến thiên theo phương trình:
\({e_1} = {E_0}{\rm{cos}}\left( {\omega t} \right);{e_2} = {E_0}{\rm{cos}}\left( {\omega t - \frac{{2\pi }}{3}} \right);{e_3} = {E_0}{\rm{cos}}\left( {\omega t + \frac{{2\pi }}{3}} \right)\). Ở thời điểm mà \({{\rm{e}}_1} = 30{\rm{\;V}}\) thì \(\left| {{e_2} - {e_3}} \right| = 30{\rm{\;V}}\). Giá trị cực đại của \({{\rm{e}}_1}\) bằng bao nhiêu vôn (Kết quả làm tròn đến 1 chữ số sau dấu phẩy).
Quảng cáo
Trả lời:
Phương pháp:
- Sử dụng công thức lượng giác xác định hiệu: \(\left| {{e_2} - {e_3}} \right|\).
- Áp dụng tính chất: \({\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha = 1\)
Cách giải:
Khi \(\left| {{e_2} - {e_3}} \right| = 30\left( V \right)\) ta có:
\(\left| {{E_0}\left[ {{\rm{cos}}\left( {\omega t - \frac{{2\pi }}{3}} \right) - {\rm{cos}}\left( {\omega t + \frac{{2\pi }}{3}} \right)} \right]} \right| = \left| {2{E_0}\sin \omega t.{\rm{sin}}\frac{{2\pi }}{3}} \right|\)
\( = \left| {\sqrt 3 {E_0}{\rm{sin}}\left( {\omega t} \right)} \right| = 30\left( V \right)\)
\( \Rightarrow \left| {{\rm{sin}}\left( {\omega t} \right)} \right| = \frac{{30}}{{\sqrt 3 {E_0}}}\)
Mà \({e_1} = {E_0}{\rm{cos}}\omega t = 30 \Rightarrow {\rm{cos}}\omega t = \frac{{30}}{{{E_0}}}\)
Lại có: \({\rm{si}}{{\rm{n}}^2}\left( {\omega t} \right) + {\rm{co}}{{\rm{s}}^2}\left( {\omega t} \right) = 1\)
\( \Rightarrow {\left( {\frac{{30}}{{\sqrt 3 {E_0}}}} \right)^2} + {\left( {\frac{{30}}{{{E_0}}}} \right)^2} = 1\)
\( \Rightarrow {E_0} = 20\sqrt 3 \left( V \right) \approx 34,6\left( V \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
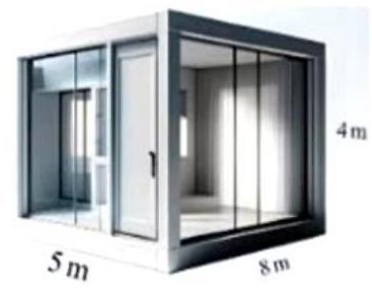
Áp dụng phương trình Clapeyron: \(pV = nRT = \frac{m}{M}RT\)
Cách giải:
Phương trình Clapeyron: \(pV = \frac{m}{M}RT \Rightarrow pV = \frac{{{\rm{\Delta }}m}}{M}.R.{\rm{\Delta }}T\)
Thay số vào ta được:
\( \Rightarrow {1,013.10^5}.4.5.8 = \frac{{{\rm{\Delta }}m}}{{29}}.8,31.\left( {20 - 0} \right)\)
\( \Rightarrow {\rm{\Delta }}m \approx {2828.10^3}\left( {\rm{g}} \right) = 2828\left( {{\rm{kg}}} \right)\)
Lời giải
Phương pháp:
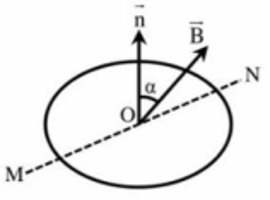
- Công thức tính từ thông: \({\rm{\Phi }} = NBS{\rm{cos}}\alpha \).
- Suất điện động cảm ứng có độ lớn: \({e_c} = N\left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B.S.{\rm{cos}}\alpha }}{{{\rm{\Delta }}t}}} \right|\)
Cách giải:
a) Ta có: \(\left( {\vec B,mp} \right) = {60^ \circ } \Rightarrow \left( {\vec B,\vec n} \right) = 90 - 60 = {30^ \circ }\)
\( \to \) a sai.
b) Từ thông gửi qua khung dây:
\({\rm{\Phi }} = NBS.\cos \alpha = {10.0,4.15.10^{ - 4}}.{\rm{cos}}30\)
\( \Rightarrow {\rm{\Phi }} \approx {5,196.10^{ - 3}}\left( {{\rm{Wb}}} \right)\)
\( \to \) b sai.
c) Khi khung dây quay quanh đường kính MN một góc \({360^ \circ }\) thì khung dây quay trở về vị trí ban đầu \( \Rightarrow {\rm{\Delta \Phi }} = 0\)
\( \to \)c sai.
d) Suất điện động cảm ứng xuất hiện trong khung dây:
\({e_c} = N\left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B.S.{\rm{cos}}\alpha }}{{{\rm{\Delta }}t}}} \right|\)
\( \Rightarrow {e_c} = 10.\left| {\frac{{\left( {0,1 - 0,04} \right){{.15.10}^{ - 4}}.{\rm{cos}}30}}{{0,05}}} \right| \approx 0,0156\left( {\rm{V}} \right)\)
Cường độ dòng điện cảm ứng xuất hiện trong khung có độ lớn:
\(i = \frac{{{e_c}}}{R} = \frac{{0,0156}}{{0,2}} = 0,78\left( A \right)\)
Câu 3
A. Giữa các phân tử có lực hút và lực đẩy gọi chung là lực liên kết phân tử.
B. Lực liên kết phân tử chỉ có lực hút, không có lực đẩy.
C. Các phân tử chuyển động không ngừng. Nhiệt độ của vật càng cao thì tốc độ chuyển động của các phân từ cấu tạo nên vật càng lớn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. bằng không.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\phi = BS{\rm{cos}}\alpha \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.