Hình bên dưới minh họa một cái lều hai mái là hai hình chữ nhật giống nhau trong không gian Oxyz. Biết các kích thước của mái lều là SA = 5m, AB = 10m, độ cao từ S xuống mặt đất là 4m. Bạn An muốn trang trí chiếc lều bằng cách treo các sợi dây cờ trang trí từ các góc lều O, A, B, C đến đuôi một chiếc đền treo từ vị trí chính giữa của SQ cách SQ 30 cm. Hỏi tổng chiều dài sợi dây cờ trang trí tối thiểu bạn An cần mua là bao nhiêu mét? (kết quả làm tròn đến hàng phần mười).
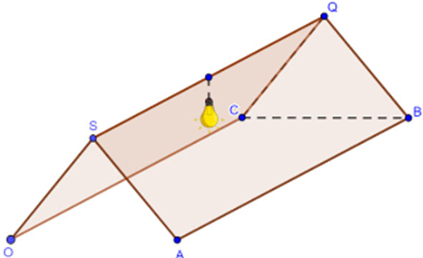
Hình bên dưới minh họa một cái lều hai mái là hai hình chữ nhật giống nhau trong không gian Oxyz. Biết các kích thước của mái lều là SA = 5m, AB = 10m, độ cao từ S xuống mặt đất là 4m. Bạn An muốn trang trí chiếc lều bằng cách treo các sợi dây cờ trang trí từ các góc lều O, A, B, C đến đuôi một chiếc đền treo từ vị trí chính giữa của SQ cách SQ 30 cm. Hỏi tổng chiều dài sợi dây cờ trang trí tối thiểu bạn An cần mua là bao nhiêu mét? (kết quả làm tròn đến hàng phần mười).
Quảng cáo
Trả lời:
Giải bởi Vietjack
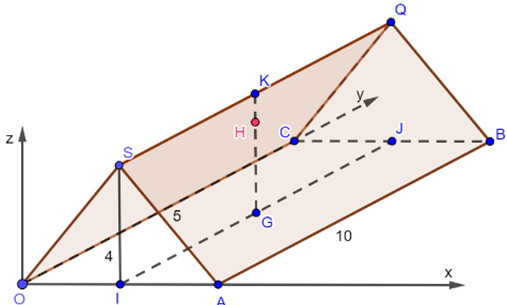
Gắn hệ trục tọa độ Oxyz như hình vẽ.
Gọi I, K lần lượt là trung điểm của OA, SQ.
\(OA = 2IA = 2\sqrt {{5^2} - {4^2}} = 6\).
Gọi H là vị trí chiếc đèn, KH = 30 cm = 0,3 m. Gọi G là giao điểm của hai đường chéo của hình chữ nhật OABC, suy ra HG = 4 – 0,3 = 3,7 m.
Do đó H(3; 5; 3,7).
Ta thấy OH = AH = CH = BH nên tổng chiều dài sợi dây màu xanh tối thiểu bạn An cần mua là 4OH.
Ta có \(\overrightarrow {OH} = \left( {3;5;3,7} \right) \Rightarrow 4OH = 4\sqrt {{3^2} + {5^2} + {{\left( {3,7} \right)}^2}} \approx 27,6\) m.
Trả lời: 27,6.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Cả hai lực tạo với nhau một góc 80° là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \), ta có \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = 50N\).
Lực còn lại là \(\overrightarrow {{F_3}} \), ta có \(\left| {\overrightarrow {{F_3}} } \right| = 60N\).
Gọi \(\overrightarrow F \) là hợp lực của ba lực trên ta có:
\(\left| {\overrightarrow F } \right| = \sqrt {{{\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right)}^2}} \)
\( = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + {{\left| {\overrightarrow {{F_3}} } \right|}^2} + 2\left( {\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right) + \left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_3}} } \right|.\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_3}} } \right) + \left| {\overrightarrow {{F_3}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \left( {\overrightarrow {{F_3}} ,\overrightarrow {{F_2}} } \right)} \right)} \)
\( = \sqrt {{{50}^2} + {{50}^2} + {{60}^2} + 2\left( {50.50.\cos 80^\circ + 50.60.\cos 60^\circ + 60.50.\cos 60^\circ } \right)} \approx 124\) N.
Trả lời: 124.
Câu 2
A. DABC cân.
B. DABC có 3 góc nhọn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có \(\overrightarrow {AB} = \left( { - 5;0; - 10} \right),\overrightarrow {AC} = \left( {3;0; - 6} \right),\overrightarrow {BC} = \left( {8;0;4} \right)\).
Ta có \(\overrightarrow {AC} .\overrightarrow {BC} = 3.8 + 0.0 + \left( { - 6} \right).4 = 0\) Þ \(\overrightarrow {AC} \bot \overrightarrow {BC} \).
Do đó DBC vuông tại C.
Câu 4
A. 1.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(ON = 6\sqrt 2 \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\overrightarrow {DC} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập