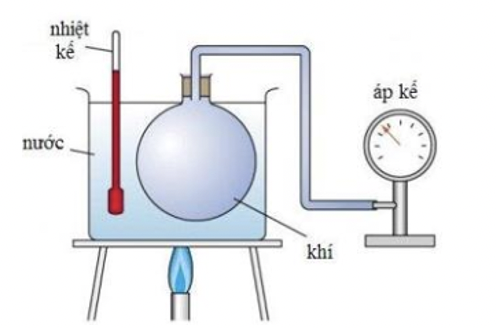
Trong một động cơ điêzen, khối khí có nhiệt độ ban đầu \({627^ \circ }{\rm{C}}\) được nén để thể tích giảm còn \(1/3\) thể tích ban đầu và áp suất tăng \(20{\rm{\% }}\) so với áp suất ban đầu. Nhiệt độ của khối khí sau khi nén bằng
A. \({251^ \circ }{\rm{C}}\)
B. \({267^ \circ }{\rm{C}}\)
C. \({87^ \circ }{\rm{C}}\)
D.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
Cách giải:
Trạng thái \(1:\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1}}\\{{T_1} = {{627}^ \circ }{\rm{C}} + 273 = 900{\rm{\;K}}}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 1,2{p_1}}\\{{V_2} = \frac{{{V_1}}}{3}}\\{{T_2} = {\rm{?\;}}}\end{array}} \right.\)
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow \frac{{{p_1}{V_1}}}{{900}} = \frac{{1,2{p_1}.\frac{{{V_1}}}{3}}}{{{T_2}}} \Rightarrow {T_2} = 360{\rm{\;K}}\)
Với \({T_2} = 360{\rm{\;K}} \Rightarrow {t_2} = {87^ \circ }{\rm{C}}\)
Chọn C.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
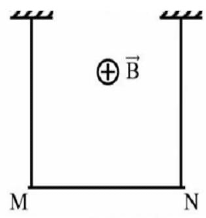
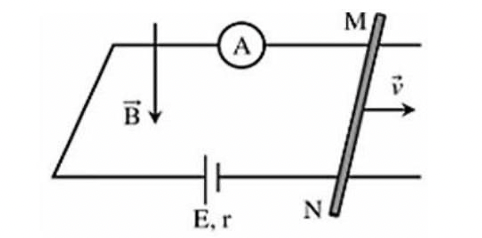
- Điều kiện cân bằng của dây.
- Lực từ tác dụng lên dây có độ lớn: \(F = BI\ell \)
Cách giải:
Lực căng dây bằng không khi đó lực từ cân bằng với trọng lực:
\(F = P \Rightarrow BI\ell = mg\)
\( \Rightarrow I = \frac{{mg}}{{B\ell }} = \frac{{0,05.10}}{{0,04}} = 12,5\left( {\rm{A}} \right)\)
Đáp án: 12,5.
Lời giải
Phương pháp:
- Áp dụng định luật Boyle: \(pV = \) const.
- Lực tác dụng lên ống thủy tinh bao gồm: Trọng lực \(\vec P\), lực đẩy Archimedes \({\vec F_A}\) và lực để giữ ống \(\vec F\).
- Áp dụng điều kiện cân bằng của vật, về độ lớn: \(P + F = {F_A}\), với \({F_A} = DVg\), V là thể tích của phần khí chiếm chỗ chất lỏng.
Cách giải:
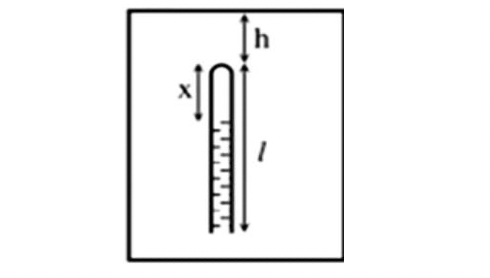
Trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1} = {p_0}}\\{{V_1} = S\ell }\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = {p_0} + h + x}\\{{V_2} = S.x}\end{array}} \right.\)
Vì nhiệt độ của khí bên trong ống không đổi nên áp dụng định luật Boyle ta được:
\({p_1}{V_1} = {p_2}{V_2} \Rightarrow 76.50 = \left( {76 + \frac{{10 + x}}{{13,6}}} \right).x\)
\( \Rightarrow x \approx 47,37\left( {{\rm{cm}}} \right)\)
Lực tác dụng lên ống thủy tinh bao gồm: Trọng lực \(\vec P\), lực đẩy Archimedes \({\vec F_A}\) và lực để giữ ống \(\vec F\).
Khi ống đứng yên ta có:
\(F + P = {F_A} \Rightarrow F = {F_A} - P = DVg - mg = DSxg - mg\)
Thay số vào ta được:
\(F = {1000.0,5.10^{ - 4}}.0,4737.10 - {15.10^{ - 3}}.10 \approx 0,09\left( N \right)\)
Đáp án: 0,09.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(T\left( K \right) = t\left( {{\;^o}C} \right) - 273\)
B. \(T\left( K \right) = t\left( {{\;^o}C} \right) + 273\)
C. \(T\left( K \right) = \frac{{t\left( {{\;^o}C} \right)}}{{273}}\)
D. \(T\left( K \right) = 273.t\left( {{\;^o}C} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo