Xác định độ biến thiên nhiệt độ của nước rơi từ độ cao 96 m xuống và đập vào cánh tuabin làm quay máy phát điện, biết rằng \(50{\rm{\% }}\) thế năng của nước làm nước nóng lên. Cho biết nhiệt dung riêng của nước là \(4190{\rm{\;J/kg}}.{\rm{K}}\). Lấy \({\rm{g}} = 10{\rm{\;m/}}{{\rm{s}}^2}\).
Xác định độ biến thiên nhiệt độ của nước rơi từ độ cao 96 m xuống và đập vào cánh tuabin làm quay máy phát điện, biết rằng \(50{\rm{\% }}\) thế năng của nước làm nước nóng lên. Cho biết nhiệt dung riêng của nước là \(4190{\rm{\;J/kg}}.{\rm{K}}\). Lấy \({\rm{g}} = 10{\rm{\;m/}}{{\rm{s}}^2}\).
Quảng cáo
Trả lời:
Phương pháp:
- Thế năng của vật ở độ cao h: \({W_t} = mgh\).
- Nhiệt lượng để làm nóng nước: \(Q = mc{\rm{\Delta }}t\).
Cách giải:
Thế năng của nước ở độ cao \({\rm{h}} = 96{\rm{\;m}}:{W_t} = mgh\)
\(50{\rm{\% }}\) thế năng của nước làm nóng nước lên, nên ta có:
\(50{\rm{\% \;}}{{\rm{W}}_t} = Q \Rightarrow 0,5.mgh = mc{\rm{\Delta }}t\)
\( \Rightarrow 0,5.10.96 = 4190.{\rm{\Delta }}t \Rightarrow {\rm{\Delta }}t \approx 0,11\)
Đáp án: 0,11.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
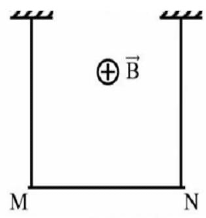
- Điều kiện cân bằng của dây.
- Lực từ tác dụng lên dây có độ lớn: \(F = BI\ell \)
Cách giải:
Lực căng dây bằng không khi đó lực từ cân bằng với trọng lực:
\(F = P \Rightarrow BI\ell = mg\)
\( \Rightarrow I = \frac{{mg}}{{B\ell }} = \frac{{0,05.10}}{{0,04}} = 12,5\left( {\rm{A}} \right)\)
Câu 2
Lời giải
Phương pháp:
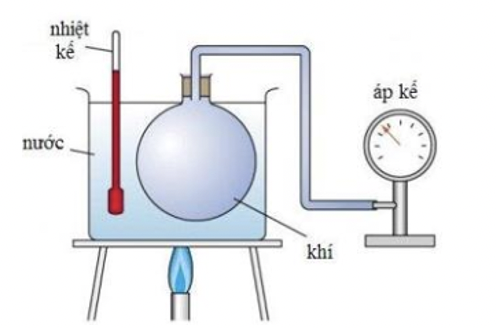
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
Cách giải:
Trạng thái \(1:\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1}}\\{{T_1} = {{627}^ \circ }{\rm{C}} + 273 = 900{\rm{\;K}}}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 1,2{p_1}}\\{{V_2} = \frac{{{V_1}}}{3}}\\{{T_2} = {\rm{?\;}}}\end{array}} \right.\)
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow \frac{{{p_1}{V_1}}}{{900}} = \frac{{1,2{p_1}.\frac{{{V_1}}}{3}}}{{{T_2}}} \Rightarrow {T_2} = 360{\rm{\;K}}\)
Với \({T_2} = 360{\rm{\;K}} \Rightarrow {t_2} = {87^ \circ }{\rm{C}}\)
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.