PHẦN III: CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u\), thì cường độ dòng điện chạy qua mạch có biểu thức là i. Đồ thị biểu diễn sự phụ thuộc của \(u\) (nét liền) và i (nét đứt) theo thời gian được cho như hình vẽ. Gọi \({\rm{U}}\left( {\rm{V}} \right)\) và \({\rm{I}}\left( {\rm{A}} \right)\) là giá trị hiệu dụng của điện áp và cường độ dòng điện, \(\varphi \) là độ lệch pha giữa điện áp và dòng điện. Tích số \({\rm{U}}{\rm{.I}}{\rm{.cos}}\varphi \) có giá trị bằng bao nhiêu Vôn.Ampe (V.A)?
PHẦN III: CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
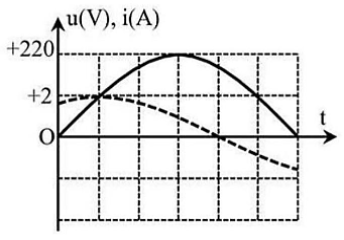
Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u\), thì cường độ dòng điện chạy qua mạch có biểu thức là i. Đồ thị biểu diễn sự phụ thuộc của \(u\) (nét liền) và i (nét đứt) theo thời gian được cho như hình vẽ. Gọi \({\rm{U}}\left( {\rm{V}} \right)\) và \({\rm{I}}\left( {\rm{A}} \right)\) là giá trị hiệu dụng của điện áp và cường độ dòng điện, \(\varphi \) là độ lệch pha giữa điện áp và dòng điện. Tích số \({\rm{U}}{\rm{.I}}{\rm{.cos}}\varphi \) có giá trị bằng bao nhiêu Vôn.Ampe (V.A)?

Quảng cáo
Trả lời:
Phương pháp:
Phân tích đồ thị xác định độ lệch pha.
Cách giải:
Điệp áp hiệu dụng: \(U = \frac{{{U_0}}}{{\sqrt 2 }} = \frac{{220}}{{\sqrt 2 }}\)
Cường độ dòng điện hiệu dụng: \(U = \frac{{{U_0}}}{{\sqrt 2 }} = \frac{{220}}{{\sqrt 2 }}\)
Dựa vào đồ thị ta thấy u trễ pha hơn i một góc \(\frac{\pi }{3}\left( {{\rm{rad}}} \right)\)
Ta có: \(UI\cos \alpha = \frac{{220}}{{\sqrt 2 }}.\frac{2}{{\sqrt 2 }}.{\rm{cos}}\frac{\pi }{3} = 110\left( W \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Vận dụng quy tắc bàn tay phải
Độ lớn lực từ: \(F = BII{\rm{sin}}\alpha \)
Cách giải:
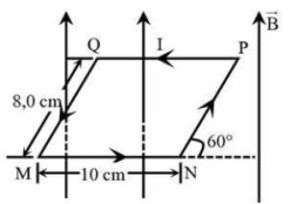
a) Lực từ tác dụng lên cạnh MN :
\({F_{MN}} = BIl{\rm{sin}}\alpha = 1,2.10.0,1.{\rm{sin}}{90^ \circ } = 1,2\left( N \right)\)
\( \to \) a sai
b) Áp dụng quy tắc bàn tay phải, lực từ tác dụng lên cạnh \(MQ\) của khung dây có chiều song song với \(\overrightarrow {NM} \).
\( \to \) b sai
c) Lực từ tác dụng lên hai cạnh MN và PQ của khung dây có độ lớn bằng nhau và ngược chiều nhau.
\( \to \) c đúng
d) Lực từ tác dụng lên cạnh NP:
\({F_{NP}} = BIl{\rm{sin}}\alpha = 1,2.10.0,08.{\rm{sin}}{30^ \circ } = 0,48\left( N \right)\)
Câu 2
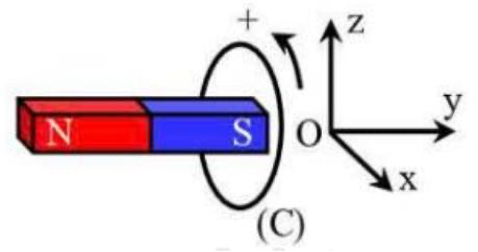
A. không có dòng điện cảm ứng.
B. có dòng điện cảm ứng chạy theo chiều dương.
C. có dòng điện cảm ứng chạy theo chiều âm.
Lời giải
Phương pháp:
Vận dụng kiến thức về dòng điện cảm ứng.
Cách giải:
Nếu cho \(\left( {\rm{C}} \right)\) quay đều theo chiều dương quanh trục quay song song với trục Oy thì trong \(\left( {\rm{C}} \right)\) không có dòng điện cảm ứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.