Một bình kín chứa 1 mol nitrogen, áp suất khí là 105 Pa, ở nhiệt độ \({27^ \circ }{\rm{C}}\). Biết hằng số khí là \({\rm{R}} = 8,31\left( {{\rm{J/mol}}.{\rm{K}}} \right)\); Hằng số Boltzmann \(k = {1,38.10^{ - 23}}\left( {{\rm{J}}/{\rm{K}}} \right)\).

     a) Thể tích của bình xấp xỉ bằng 25 lít.

     b) Nung bình đến khi áp suất khí bằng \({5.10^5}{\rm{\;Pa}}\). Nhiệt độ của khối khí khi đó là \({135^ \circ }{\rm{C}}\)

     c) Động năng trung bình của phân tử khí ở nhiệt độ \({27^ \circ }{\rm{C}}\) bằng \({2,76.10^{ - 21}}\left( {{\rm{\;J}}} \right)\)

     d) Giả sử một lượng khí thoát ra ngoài nên áp suất khí trong bình giảm còn \({4.10^5}{\rm{\;Pa}}\), nhiệt độ khí lúc này là \({1227^ \circ }{\rm{C}}\). Lượng khí đã thoát ra ngoài là \(0,2{\rm{\;mol}}\).

Sử dụng bảng số liệu dưới đây. Cần bao nhiêu thời gian (s) để làm nóng chảy hoàn toàn 2 kg đồng có nhiệt độ ban đầu \({30^ \circ }{\rm{C}}\), trong một lò nung điện công suất 20000 W. Biết chỉ có \(50{\rm{\% }}\) năng lượng tiêu thụ của lò được dùng vào việc làm đồng nóng lên và nóng chảy hoàn toàn ở nhiệt độ không đổi. Biết nhiệt dung riêng của đồng là \(380{\rm{\;J/kg}}{\rm{.K}}\). (Kết quả làm tròn đến phần nguyên)

Phát biểu nào sau đây là sai khi nói về nhiệt hoá hơi?

PHẦN II: CÂU TRẮC NGHIỆM ĐÚNG SAI

 Một ấm điện có công suất 1000 W chứa 300 g nước ở \({20^ \circ }{\rm{C}}\) đến khi sôi ở áp suất tiêu chuẩn. Cho nhiệt dung riêng và nhiệt hóa hơi riêng của nước lần lượt là \({4,2.10^3}{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\) và \({2,26.10^6}{\rm{\;J}}/{\rm{kg}}\).

     a) Nhiệt lượng để làm nóng 300 g nước từ \({20^ \circ }{\rm{C}}\) đến \({100^ \circ }{\rm{C}}\) là 100800 J

     b) Nhiệt lượng cần cung cấp để 200 g nước hỏa hơi hoàn toàn ở \({100^ \circ }{\rm{C}}\) là \({678.10^6}{\rm{\;J}}\)

     c) Thời gian cần thiết để đun nước trong ẩm đạt đến nhiệt độ sôi là 100,8 phút

     d) Sau khi nước đến nhiệt độ sôi, người ta để ấm tiếp tục đun nước sôi trong 226 s. Khối lượng nước còn lại trong ẩm xấp xỉ 100 g.

Dòng điện do một máy phát điện tạo ra có cường độ biến thiên theo thời gian được cho trong hình dưới đây.

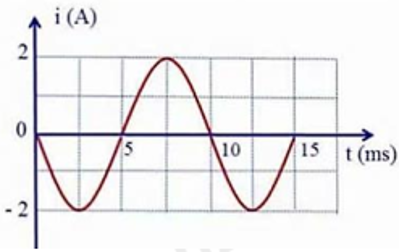
     a) Dòng điện được tạo ra là dòng điện xoay chiều.

     b) Chu kì của dòng điện là 5 s.

     c) Cường độ dòng điện hiệu dụng có giá trị \(\sqrt 2 \left( A \right)\).

     d) Phương trình của dòng điện là \(i = 2{\rm{cos}}\left( {200\pi t + \frac{\pi }{2}} \right)\left( A \right)\)

Hình vẽ sau đây biểu diễn sự thay đổi độ phóng xạ của một mẫu chất phóng xạ \({\beta ^ - }\)theo thời gian.

     a) Sau 4,5 giờ từ thời điểm ban đầu, độ phóng xạ của mẫu là 10 kBq.

     b) Chu kì bán rã của chất phóng xạ là 1,5 giờ.

     c) Trong 3 giờ đầu, mẫu chất phát ra 20000 hạt electron.

     d) Kể từ thời điểm ban đầu, số hạt nhân chất phóng xạ còn lại trong mẫu sau 9 giờ bằng 1/64 số hạt nhân chất phóng xạ ban đầu.

Một nhà máy điện hạt nhân có công suất phát điện là 1200 MW và hiệu suất phát điện là \(32{\rm{\% }}\). Nhà máy sử dụng các thanh nhiên liệu hạt nhân \(\;_{92}^{235}U\) được làm giàu \(25{\rm{\% }}\) (nghĩa là \(\;_{92}^{235}U\) chiếm \(25{\rm{\% }}\) khối lượng thanh nhiên liệu). Biết rằng mỗi phân hạch của hạt nhân \(\;_{92}^{235}U\) tỏa năng lượng 200 MeV. Cho số Avogadro \({N_A} \approx {6,022.10^{ - 23}}{\rm{\;mo}}{{\rm{l}}^{ - 1}}\) và khối lượng mol của nguyên tử của \(\;_{92}^{235}U\) là \(235{\rm{\;g/mol}}\). Khối lượng nhiên liệu nhà máy sử dụng trong một năm (365 ngày) là bao nhiêu kg? (Kết quả làm tròn đến phần nguyên).