Xét một lượng khí lý tưởng xác định. Biết khối lượng riêng của không khí ở \({0^ \circ }{\rm{C}}\), áp suất \({10^5}{\rm{\;Pa}}\) là \(1,29{\rm{\;kg/}}{{\rm{m}}^3}\). Khối lượng riêng của không khí ở \({100^ \circ }{\rm{C}}\), áp suất \({2.10^5}{\rm{\;Pa}}\) xấp xỉ là
Quảng cáo
Trả lời:
Phương pháp:
Phương trình Clapeyron theo khối lượng riêng: \(\frac{p}{{TD}} = \frac{R}{M}\).
Cách giải:
Áp dụng phương trình Clapeyron theo khối lượng riêng ta được:
\(\frac{{{p_1}}}{{{p_2}}} = \frac{{{T_1}}}{{{T_2}}}.\frac{{{D_1}}}{{{D_2}}} \Rightarrow \frac{{{{10}^5}}}{{{{2.10}^5}}} = \frac{{0 + 273}}{{100 + 273}}.\frac{{1,29}}{{{D_2}}}\)
\( \Rightarrow {D_2} \approx 1,89\left( {{\rm{kg}}/{{\rm{m}}^3}} \right)\)
Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Áp dụng nguyên lý Pascal: Các điểm nằm trong cùng một chất lỏng ở trên cùng một mặt phẳng thì có cùng áp suất.
Áp suất do cột chất lỏng gây ra: \(p = dh\), d là trọng lượng riêng của chất lỏng.
Áp dụng phương trình trạng thái khí lý tưởng: \(\frac{{pV}}{T} = \) const.
Cách giải:
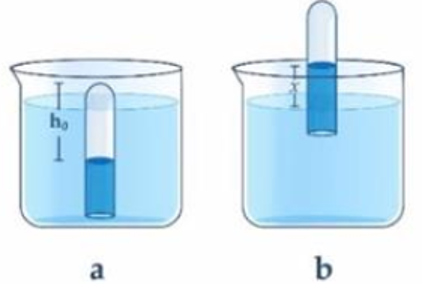
a) Áp suất của khối khí khi nhúng vào chậu (hình a) là:
\(p = {p_0} + dh = {9,8.10^4} + {10^4}.0,2 = {10^5}\left( {{\rm{Pa}}} \right)\)
\( \to {\rm{a}}\) đúng.
b) Trạng thái (a): \(\left\{ {\begin{array}{*{20}{l}}{{p_a} = {p_0} + dh = {{10}^5}\left( {Pa} \right)}\\{{V_a} = S.{h_0} = S.20}\\{{T_a} = 27 + 273 = 300\left( K \right)}\end{array}} \right.\)
Trạng thái (b): \(\left\{ {\begin{array}{*{20}{l}}{{p_b} = {p_0} = {{9,8.10}^4}\left( {Pa} \right)}\\{{V_b} = S.30}\\{{T_b} = {t_b} + 273}\end{array}} \right.\)
Áp dụng phương trình trạng thái của khí lý tưởng:
\(\frac{{{p_a}{V_a}}}{{{T_a}}} = \frac{{{p_b}{V_b}}}{{{T_b}}} \Rightarrow \frac{{{{10}^5}.20}}{{300}} = \frac{{{{9,8.10}^4}.30}}{{{t_b} + 273}}\)
\( \Rightarrow {t_b} = 168\left( {{\;^{\rm{o}}}{\rm{C}}} \right)\)
\( \to {\rm{b}}\) đúng.
c) Sau khi kéo ống lên, gọi \(x\) là độ chênh lệch giữa hai mực chất lỏng trong và ngoài ống (\(x > 0\) nếu chất lỏng bên trong cao hơn, x tính bằng m)
Trạng thái (b'): \(\left\{ {\begin{array}{*{20}{l}}{{p_{b'}} = {p_0} - d.x = {{9,8.10}^4} - {{10}^4}.x\left( {Pa} \right)}\\{{V_{b'}} = S.\left( {0,3 - x} \right)}\end{array}} \right.\)
Vì nhiệt độ không đổi nên áp dụng định luật Boyle:
\({p_a}{V_a} = {p_{b'}}{V_{b'}} \Rightarrow {10^5}.0,2 = \left( {{{9,8.10}^4} - {{10}^4}.x} \right).\left( {0,3 - x} \right)\)
\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{x \approx 0,096\left( {\rm{m}} \right) = 9,6\left( {{\rm{cm}}} \right)}\\{x = 10\left( {\rm{m}} \right) > 30\left( {{\rm{cm}}} \right)\left( L \right)}\end{array}} \right.\)
\( \to \) c sai.
d) Áp suất của khí trong ống không luôn bằng áp suất do cột nước gây ra. Ví dụ như câu a) nó còn có thêm áp suất khí quyển.
\( \to \) d sai.
Lời giải
Phương pháp:
- Viết phương trình đồ thị biểu diễn công suất tỏa nhiệt ra môi trường và thời gian.
- Tính công suất tỏa nhiệt ra môi trường trung bình: \(\overline P = \frac{{{P_0} + P}}{2}\)
- Áp dụng phương trình cân bằng nhiệt.
Cách giải:
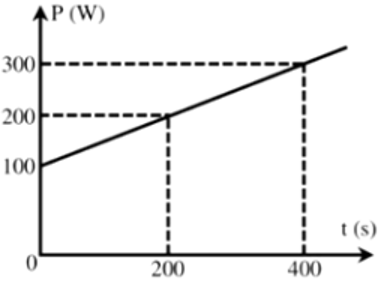
Phương trình đồ thị: \(P = at + b\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{300 = a.400 + b}\\{100 = a.0 + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 0,5}\\{b = 100}\end{array}} \right.} \right.\)
\( \Rightarrow P = 0,5t + 100\)
Công suất tỏa nhiệt trung bình ra môi trường:
\(\overline P = \frac{{{P_0} + P}}{2} = \frac{{100 + 0,5t + 100}}{2} = 100 + 0,25t\)
Áp dụng phương trình cân bằng nhiệt:
\({P_{tp}}t = \overline P t + mc{\rm{\Delta }}t\)
Thay số vào ta được:
\(500t = \left( {0,25t + 100} \right).t + 2.4200.10 \Rightarrow t \approx 249\left( s \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.