Một lượng khí He lí tưởng đựng trong một xi lanh, pittông nhẹ có thể chuyển động không ma sát dọc theo xi lanh như hình vẽ. Tiết diện của pit-tông là \({8.10^{ - 3}}\;{{\rm{m}}^2}\).
Một đầu pit-tông được gắn với lò xo có độ cứng \({8.10^3}\;{\rm{N}}/{\rm{m}}\). Ban đầu pit-tông nằm cân bằng, lò xo không biến dạng, khí ở nhiệt độ 300 K và có thể tích \({2,4.10^{ - 3}}\;{{\rm{m}}^3}\). Khí được nung nóng cho đến khi pit-tông dịch chuyển chậm ra ngoài một đoạn \(0,15\;{\rm{m}}\). Biết áp suất khí quyển là \({10^5}\;{\rm{N}}/{{\rm{m}}^2}\).
a) Áp suất của khí trong xi lanh sau khi bị nung nóng là \(2 \cdot {10^5}\;{\rm{N}}/{{\rm{m}}^2}\).
b) Thể tích của khối khí sau khi bị nung nóng là \({3,6.10^{ - 3}}\;{{\rm{m}}^3}\).
c) Nhiệt độ cuối cùng của khí là 1125 K.
d) Nhiệt lượng mà khối khí nhận được 1020 J.
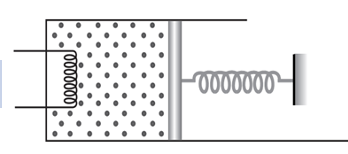
Một lượng khí He lí tưởng đựng trong một xi lanh, pittông nhẹ có thể chuyển động không ma sát dọc theo xi lanh như hình vẽ. Tiết diện của pit-tông là \({8.10^{ - 3}}\;{{\rm{m}}^2}\).
Một đầu pit-tông được gắn với lò xo có độ cứng \({8.10^3}\;{\rm{N}}/{\rm{m}}\). Ban đầu pit-tông nằm cân bằng, lò xo không biến dạng, khí ở nhiệt độ 300 K và có thể tích \({2,4.10^{ - 3}}\;{{\rm{m}}^3}\). Khí được nung nóng cho đến khi pit-tông dịch chuyển chậm ra ngoài một đoạn \(0,15\;{\rm{m}}\). Biết áp suất khí quyển là \({10^5}\;{\rm{N}}/{{\rm{m}}^2}\).
a) Áp suất của khí trong xi lanh sau khi bị nung nóng là \(2 \cdot {10^5}\;{\rm{N}}/{{\rm{m}}^2}\).
b) Thể tích của khối khí sau khi bị nung nóng là \({3,6.10^{ - 3}}\;{{\rm{m}}^3}\).
c) Nhiệt độ cuối cùng của khí là 1125 K.
d) Nhiệt lượng mà khối khí nhận được 1020 J.

Quảng cáo
Trả lời:
\(p = {p_0} + \frac{{k\Delta l}}{S} = {10^5} + \frac{{8 \cdot {{10}^3} \cdot 0,15}}{{8 \cdot {{10}^{ - 3}}}} = 2,5 \cdot {10^5}\;{\rm{Pa}}(1) \Rightarrow \) a) Sai
\(V = {V_0} + S\Delta l = 2,4 \cdot {10^{ - 3}} + 8 \cdot {10^{ - 3}} \cdot 0,15 = 3,6 \cdot {10^{ - 3}}{m^3}(2) \Rightarrow \) b) Đúng
\(\frac{{pV}}{T} = \frac{{{p_0}{V_0}}}{{{T_0}}} \Rightarrow \frac{{2,5 \cdot {{10}^5} \cdot 3,6 \cdot {{10}^{ - 3}}}}{T} = \frac{{{{10}^5} \cdot 2,4 \cdot {{10}^{ - 3}}}}{{300}} \Rightarrow T = 1125\;{\rm{K}} \Rightarrow \) c) Đúng
Heli là khí đơn nguyên tử nên
\(\Delta U = \frac{3}{2}nR\Delta T = \frac{3}{2}\left( {pV - {p_0}{V_0}} \right) = \frac{3}{2} \cdot \left( {2,5 \cdot {{10}^5} \cdot 3,6 \cdot {{10}^{ - 3}} - {{10}^5} \cdot 2,4 \cdot {{10}^{ - 3}}} \right) = 990J\)
Cách 1: Từ (1) và (2) \( \Rightarrow p = {p_0} + \frac{{k\Delta l}}{S} = {p_0} + \frac{{k\left( {V - {V_0}} \right)}}{{{S^2}}} = {10^5} + \frac{{{{8.10}^3}\left( {V - {{2,4.10}^{ - 3}}} \right)}}{{{{\left( {{{8.10}^{ - 3}}} \right)}^2}}}\)
\({A^\prime } = \int_{{V_1}}^{{V_2}} p dV = \int_{{{2,4.10}^{ - 3}}}^{{{3,6.10}^{ - 3}}} {\left( {{{10}^5} + \frac{{{{8.10}^3}\left( {V - {{2,4.10}^{ - 3}}} \right)}}{{{{\left( {{{8.10}^{ - 3}}} \right)}^2}}}} \right)} dV = 210J\)
Cách 2: \({A^\prime } = {A_{kq}} + {A_{dh}} = {p_0}\left( {V - {V_0}} \right) + \frac{1}{2}k\Delta {l^2} = {10^5} \cdot (3,6 - 2,4) \cdot {10^{ - 3}} + \frac{1}{2} \cdot 8 \cdot {10^3} \cdot {0,15^2} = 210\;{\rm{J}}\) \(Q = \Delta U + {A^\prime } = 990 + 210 = 1200\;{\rm{J}} \Rightarrow \) d) Sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
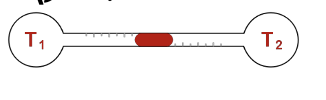
A. Dịch chuyển sang phía có nhiệt độ lớn hơn.
B. Nằm yên không dịch chuyển.
Lời giải
\(\left\{ {\begin{array}{*{20}{l}}{\frac{{pV}}{{{T_1}}} = \frac{{{p^\prime }{V_1}}}{{2{T_1}}}}\\{\frac{{pV}}{{{T_2}}} = \frac{{{p^\prime }{V_2}}}{{2{T_2}}}}\end{array} \Rightarrow pV = \frac{{{p^\prime }{V_1}}}{2} = \frac{{{p^\prime }{V_2}}}{2} \Rightarrow {V_1} = {V_2} \Rightarrow } \right.\) giọt thủy ngân nằm yên. Chọn B
Lời giải
Lần 1: \({p_0}V = {p_1}\left( {V + \frac{V}{{20}}} \right) \Rightarrow {p_1} = \frac{{20{p_0}}}{{21}}\)
Lần 2: \({p_1}V = {p_2}\left( {V + \frac{V}{{20}}} \right) \Rightarrow {p_2} = \frac{{20{p_1}}}{{21}} = {\left( {\frac{{20}}{{21}}} \right)^2}{p_0}\)
Tương tự cho đến lần n thì \({p_n} = {\left( {\frac{{20}}{{21}}} \right)^n}{p_0} = {\left( {\frac{{20}}{{21}}} \right)^n}.760 < 5 \Rightarrow n > 102,97 \Rightarrow {n_{\min }} = 103\)
Trả lời ngắn: 103
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.