Một mol khí lí tưởng biến đổi trạng thái theo chu trình ABC như Hình 2. Nhiệt độ của khí ở trạng thái A là \({{\rm{T}}_0} = 250\;{\rm{K}}\). Hai điểm \({\rm{B}},{\rm{C}}\) cùng nằm trên một đường đẳng nhiệt, đường thẳng AC đi qua gốc tọa độ O. Nhiệt độ cực đại mà khí đạt được khi biến đổi theo chu trình trên bằng bao nhiêu độ K ?
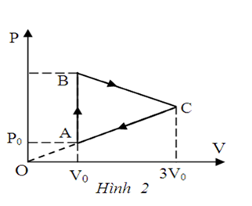
Một mol khí lí tưởng biến đổi trạng thái theo chu trình ABC như Hình 2. Nhiệt độ của khí ở trạng thái A là \({{\rm{T}}_0} = 250\;{\rm{K}}\). Hai điểm \({\rm{B}},{\rm{C}}\) cùng nằm trên một đường đẳng nhiệt, đường thẳng AC đi qua gốc tọa độ O. Nhiệt độ cực đại mà khí đạt được khi biến đổi theo chu trình trên bằng bao nhiêu độ K ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
\(\frac{{pV}}{T} = \) const \( \Rightarrow {T_{\max }}\) thì \({(pV)_{\max }} \Rightarrow \) trạng thái đó nằm trên đoạn BC
Theo Talet có \({p_C} = 3{p_0}\) và \({T_B} = {T_C} \Rightarrow {p_B}{V_B} = {p_C}{V_C} \Rightarrow {p_B} \cdot {V_0} = 3{p_0} \cdot 3{V_0} \Rightarrow {p_B} = 9{p_0}\)
\[{T_B} = {T_C}\] thì \[{\rm{ }}{T_{\max }}\] sẽ ở trung điểm của \[{\rm{BC}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{V = \frac{{{V_B} + {V_C}}}{2} = \frac{{{V_0} + 3{V_0}}}{2} = 2{V_0}}\\{p = \frac{{{p_B} + {p_C}}}{2} = \frac{{3{p_0} + 9{p_0}}}{2} = 6{p_0}}\end{array}} \right.\]
\[\frac{{pV}}{T} = \frac{{{p_0}{V_0}}}{{{T_0}}} \Rightarrow \frac{{6{p_0} \cdot 2{V_0}}}{{{T_{\max }}}} = \frac{{{p_0}{V_0}}}{{250}} \Rightarrow {T_{\max }} = 3000\;{\rm{K}}\]
Trả lời ngắn: 3000
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Truyền nhiệt lượng Q cho khối khí nên \(Q > 0 \Rightarrow \) a) Sai
Thể tích của khối khí tăng thêm 7,0 lít \( \Rightarrow \) b) Sai
\(|A| = p\Delta V = 3 \cdot {10^5} \cdot 7 \cdot {10^{ - 3}} = 2100\;{\rm{J}} \Rightarrow \) c) Đúng
\(\Delta U = Q + A \Rightarrow - 1100 = Q - 2100 \Rightarrow Q = {10^3}\;{\rm{J}} \Rightarrow \) d) Đúng
Câu 2
A. Hình 1.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đẳng áp và thể tích giảm. Chọn C
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. độ Celsius (kí hiệu ).
B. độ Kelvin (kí hiệu K ) và độ Celsius (kí hiệu ).
C. độ Kelvin (kí hiệu K).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập