Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d)
Cho hình thang \(ABCD{\rm{ }}\left( {AB\parallel CD} \right)\). Một đường thẳng song song với hai đáy, cắt các cạnh bên \(AD\) và \(BC\) theo thứ tự \(M\) và \(N.\) Gọi \(I\) là giao điểm của đường chéo \(AC\) với \(MN\). Khi đó:
a) \(\frac{{AM}}{{MD}} = \frac{{AI}}{{IC}}.\)
b) \(\frac{{AM}}{{MD}} = \frac{{BN}}{{BC}}.\)
c) \(\frac{{CN}}{{CB}} = \frac{{CI}}{{CA}}.\)
d) \(\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = 1\).
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d)
Cho hình thang \(ABCD{\rm{ }}\left( {AB\parallel CD} \right)\). Một đường thẳng song song với hai đáy, cắt các cạnh bên \(AD\) và \(BC\) theo thứ tự \(M\) và \(N.\) Gọi \(I\) là giao điểm của đường chéo \(AC\) với \(MN\). Khi đó:
a) \(\frac{{AM}}{{MD}} = \frac{{AI}}{{IC}}.\)
b) \(\frac{{AM}}{{MD}} = \frac{{BN}}{{BC}}.\)
c) \(\frac{{CN}}{{CB}} = \frac{{CI}}{{CA}}.\)
d) \(\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = 1\).Quảng cáo
Trả lời:
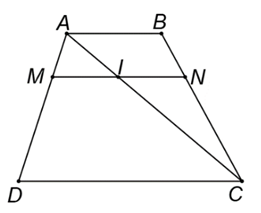
a) Đúng.
Áp dụng định lí Thalès vào tam giác \(ACD\)có \(IM\parallel CD\) ta được: \(\frac{{AM}}{{MD}} = \frac{{AI}}{{IC}}.\) (1)
b) Sai.
Áp dụng định lí Thalès vào tam giác \(ACB\) có \(IN\parallel AB\) ta được: \(\frac{{BN}}{{NC}} = \frac{{AI}}{{IC}}.\) (2)
Từ (1) và (2) suy ra \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}.\)
c) Đúng.
Áp dụng định lí Thalès vào tam giác \(ACB\) có \(IN\parallel AB\) ta được: \(\frac{{CN}}{{CB}} = \frac{{IC}}{{AC}}.\) (3)
d) Đúng.
Áp dụng định lí Thalès vào tam giác \(ACD\) có \(IM\parallel CD\) ta được: \(\frac{{AM}}{{AD}} = \frac{{AI}}{{AC}}.\) (4)
Cộng theo vế các đẳng thức (3) và (4) thu được:
\(\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = \frac{{AI}}{{AC}} + \frac{{IC}}{{AC}} = \frac{{AI + IC}}{{AC}} = \frac{{AC}}{{AC}} = 1.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
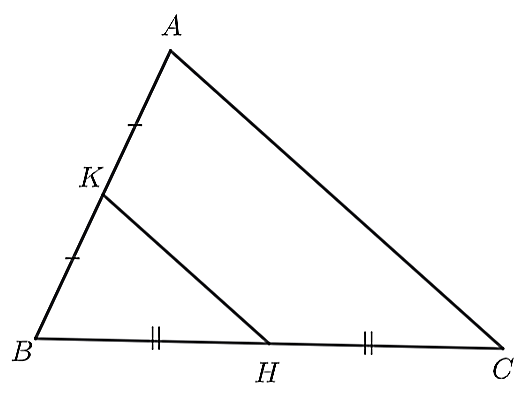
Câu 1
A. \(HK\parallel BC.\)
Lời giải
Đáp án đúng là: A
Câu 2
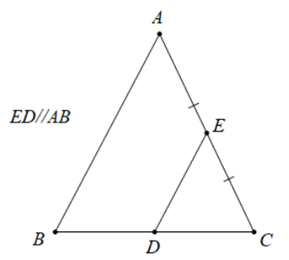
A. \(AE = \frac{1}{2}BC.\)
B. \(D\) là trung điểm của \(BC.\)
Lời giải
Đáp án đúng là: B
Từ hình vẽ, ta có \(ED\parallel AB\) và \(E\) là trung điểm \(AC\) nên \(DE\) là đường trung bình của \(\Delta ABC\).
Do đó, \(D\) là trung điểm của \(BC.\)
Câu 3
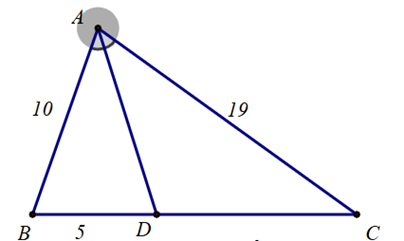
A. \(\frac{{AB}}{{CD}} = \frac{1}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
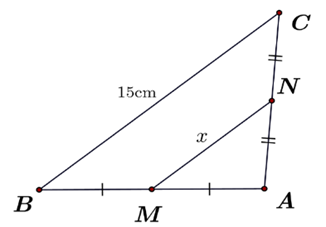
A. 20 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
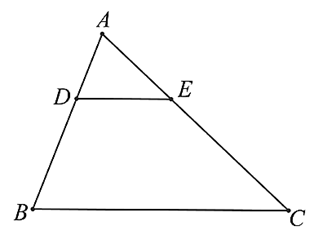
A. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC\)
B. \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) suy ra \(DE\parallel BC\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{3}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.