Cặp số nào dưới đây là thuộc đường thẳng biểu diễn nghiệm của phương trình \[2x--5y = 19?\]
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
• Thay \[x = 2,{\rm{ }}y = - 3\] vào phương trình \[2x--5y = 19\] ta được: \[2 \cdot 2--5 \cdot \left( { - 3} \right) = 19.\]
Do đó cặp số \[\left( {2\,;\,\, - 3} \right)\] thuộc đường thẳng biểu diễn nghiệm của phương trình đã cho.
• Thay x = 1, y = 1 vào phương trình \[2x--5y = 19\] ta được: \[2 \cdot 1--5 \cdot 1 = 7 \ne 19.\]
Do đó, cặp số \[\left( {1\,;\,\,1} \right)\] không thuộc đường thẳng biểu diễn nghiệm của phương trình đã cho.
• Thay \[x = 1,{\rm{ }}y = - 2\] vào phương trình \[2x--5y = 19\] ta được: \[2 \cdot 1--5 \cdot \left( { - 2} \right) = 12 \ne 19.\]
Do đó, cặp số \[\left( {1\,;\,\, - 2} \right)\] không thuộc đường thẳng biểu diễn nghiệm của phương trình đã cho.
• Thay \[x = 12,{\rm{ }}y = - 1\] vào phương trình \[2x--5y = 19\] ta được \[2 \cdot 12 - 5 \cdot \left( { - 1} \right) = 27 \ne 19.\]
Do đó, cặp số \[\left( {12\,;\,\, - 1} \right)\] không thuộc đường thẳng biểu diễn nghiệm của phương trình đã cho.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
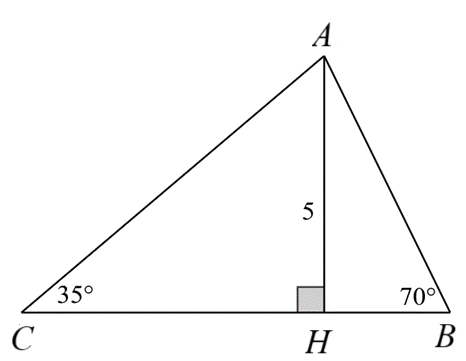
1) Xét tam giác \(AHB\) vuông tại \(H\) nên \(\sin B = \frac{{AH}}{{AB}}\) Suy ra \(AB = \frac{{AH}}{{\sin B}} = \frac{5}{{\sin 70^\circ }} \approx 5,32\,\,\left( {{\rm{cm}}} \right)\) Xét tam giác \(AHC\) vuông tại \(H\) nên \(\sin C = \frac{{AH}}{{AC}}\) Suy ra \(AC = \frac{{AH}}{{\sin C}} = \frac{5}{{\sin 35^\circ }} \approx 8,72\,\,\left( {{\rm{cm}}} \right)\) |
|
Áp dụng hệ thức giữa cạnh huyền và cạnh góc vuông trong tam giác vuông, ta có
\(BH = AH \cdot \cot B = 5 \cdot \cot 70^\circ \approx 1,82\,\,\left( {{\rm{cm}}} \right)\)
\(CH = AH \cdot \cot C = 5 \cdot \cot 35^\circ \approx 7,14\,\,\left( {{\rm{cm}}} \right)\)
Do đó \(BC = BH + HC \approx 1,82 + 7,14 = 8,96\,\,\left( {{\rm{cm}}} \right)\)
Vậy độ dài các cạnh của tam giác \(ABC\) là \(AB \approx 5,32\,\,{\rm{cm}}\,{\rm{,}}\,\,AC \approx 8,72\,\,{\rm{cm}}\,{\rm{,}}\,\,BC \approx 8,96\,\,{\rm{cm}}\,.\)
|
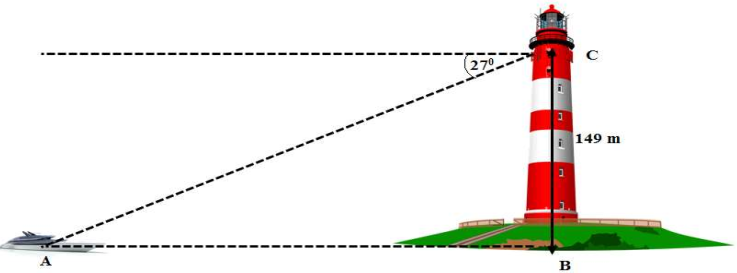
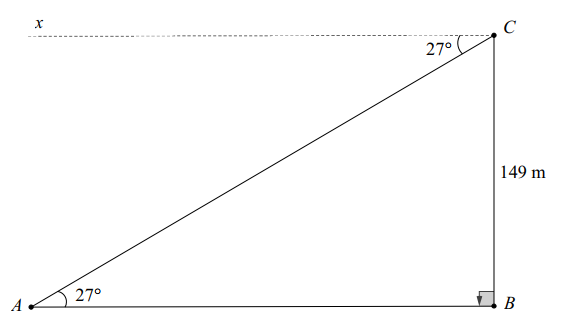
2) Giả sử trong hình vẽ \(BC\) là độ cao của ngọn hải đăng so với mực nước biển thì \(AB\) là khoảng cách từ tàu đến chân ngọn hải đăng, góc nghiêng xuống \[\widehat {ACx} = 27^\circ \] nên \[\widehat {CAB} = 27^\circ .\] Xét \(\Delta ABC\) vuông tại \(B\) có \(AB = BC \cdot \cot \widehat {CAB}\). Suy ra \[AB = 149 \cdot \cot 27^\circ \approx 292\,\,\left( {\rm{m}} \right)\]. |
|
Vậy tàu đang đứng cách chân hải đăng khoảng 292 mét.
Lời giải
Hướng dẫn giải
Đáp án: 3.
Cách 1. Sử dụng MTCT để tìm nghiệm của hệ hai phương trình \(\left\{ \begin{array}{l}x - y = 1\\3x + y = 7\end{array} \right.\).
Với MTCT phù hợp, ta bấm lần lượt các phím:
Trên màn hình cho kết quả \(x = 2,\) ta bấm tiếp phím màn hình cho kết quả \(y = 1.\)
Do đó \[x + y = 2 + 1 = 3.\]
Cách 2. Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\3x + y = 7\end{array} \right.\)
Cộng từng vế hai phương trình của hệ phương trình trên, ta được: \(4x = 8\), suy ra \(x = 2.\)
Thay \(x = 2\) vào phương trình \(x - y = 1,\) ta được: \(2 - y = 1,\) suy ra \(y = 1.\)
Do đó \[x + y = 2 + 1 = 3.\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[a \le 3,2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.