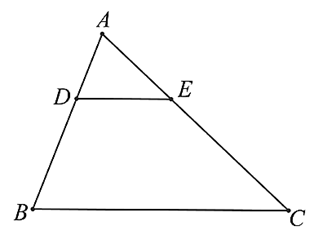
Cho tam giác \(ABC\) nhọn có đường cao \(AH\). Trên \(AH\) lấy các điểm \(K,I\) sao cho \(AK = KI = IH.\) Qua \(K,I\) lần lượt vẽ các đường thẳng \(MN\parallel BC,{\rm{ }}EF\parallel BC\) (\(M,E \in AB,\) \(N,F \in AC\)).

a) \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}.\)

b) \(\frac{{EF}}{{BC}} = \frac{3}{2}.\)

c) \(MNEF\) là hình bình hành.

d) Biết \({S_{ABC}} = 90{\rm{ c}}{{\rm{m}}^2},\) khi đó \({S_{MNEF}} = 30{\rm{ c}}{{\rm{m}}^2}.\)

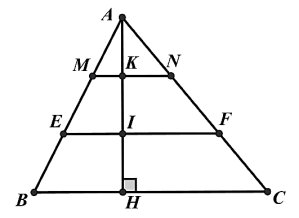
a) Đúng.

Áp dụng định lí Thalès vào tam giác \(ABC\) có \(MN\parallel BC\) ta được: \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\) suy ra \(\frac{{MN}}{{BC}} = \frac{1}{3}\).

b) Sai.

Áp dụng định lí Thalès vào tam giác \(ABC\) có \(EF\parallel BC\) ta được: \(\frac{{EF}}{{BC}} = \frac{{AF}}{{AC}}\) suy ra \(\frac{{EF}}{{BC}} = \frac{2}{3}\).

c) Đúng.

Xét tứ giác \(MNFE\) có \(MN\parallel BC\) và \(KI \bot MN\). Do đó \(MNFE\) là hình thang có hai đáy \(MN,FE\) và chiều cao \(KI.\)

d) Đúng.

Ta có: \({S_{MNEF}} = \frac{{\left( {MN + FE} \right) \cdot KI}}{2} = \frac{{\left( {\frac{1}{3}BC + \frac{2}{3}BC} \right) \cdot \frac{1}{3}AH}}{2} = \frac{1}{3}{S_{ABC}} = 30{\rm{ c}}{{\rm{m}}^2}.\)